cho đương tròn tâm O , M ngoài đường tròn vẽ tiếp tuyến MA và MC . Vẽ dây cung BC song song MA, BM cắt (O) tại D , CD cắt AM tại I . Chứng minh
a) IM2= IC x ID
b) I là trung điểm AM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
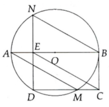
b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN
Do BCDE là hình bình hành
=> BC = ED; DE = EN
=> BA ⊥ EN => BABC
=> BC là tiếp tuyến

a) Ta có \(\widehat{AND}=\widehat{AMD}\)(góc nội tiếp cùng chắn cung AD)
\(AM//BN\Rightarrow\widehat{AMN}=\widehat{MNB}\left(slt\right)\)
Ta có góc ANB nội tiếp đường trong O chắn nửa đường trong => góc ANB=900
Ta có: \(\widehat{AMD}+\widehat{AMN}+\widehat{DNM}=\widehat{DNM}+\widehat{AND}+\widehat{MNB}\)
\(\Leftrightarrow\widehat{DMN}+\widehat{MND}=90^0\Leftrightarrow\widehat{NDM}=90^0\)
Vì DM//AB và ND vuông góc với DM => DN vuông góc với AB
b) Ta có \(\widehat{BAN}=\widehat{BMN}\)(cùng chắn cung BN)
Mà \(\widehat{AMN}+\widehat{NMB}=90^0\Rightarrow\widehat{BAN}+\widehat{BAM}=90^0\Rightarrow\widehat{MAN}=90^0\)
\(\Rightarrow MANB\)là hcn
=> AM=BN
Ta có MC//AE và AM//EC => AMCE là hbh => AM=EC mà AM=BN => BN=EC mà BN//EC => ENBC là hbh =>EN//CB => CB vuông góc với AB(vì AB vuông góc với EN)=> BC là tiếp tuyến của đường tròn O
Chúc bạn học tốt!!!
xem lời giải ở đâu
a: MA//BC
OA vuông góc AM
=>OA vuông góc BC
OB=OC
=>O thuộc trung trực của BC
=>OA là trung trực của BC
=>sđ cung AB=sđ cung AC
góc AMC=1/2(sđ cung ABC-sđ cung AC)
=1/2 sđ BC
góc BDC=1/2*sđ cung BC
=>góc AMC=góc BDC
mà góc BDC=góc IDM
nên góc AMC=góc IDM
=>góc IMC=góc IDM
mà góc MIC chung
nên ΔIMC đồng dạng với ΔIDM
=>IM/ID=IC/IM
=>IM^2=ID*IC
b: Xét ΔIAD và ΔICA có
gócIAD=góc ICA
góc AID chung
=>ΔIAD đồng dạng vơi ΔICA
=>IA/IC=ID/IA
=>IA^2=IC*ID=IM^2
=>IA=IM
=>I là trung điểm của AM