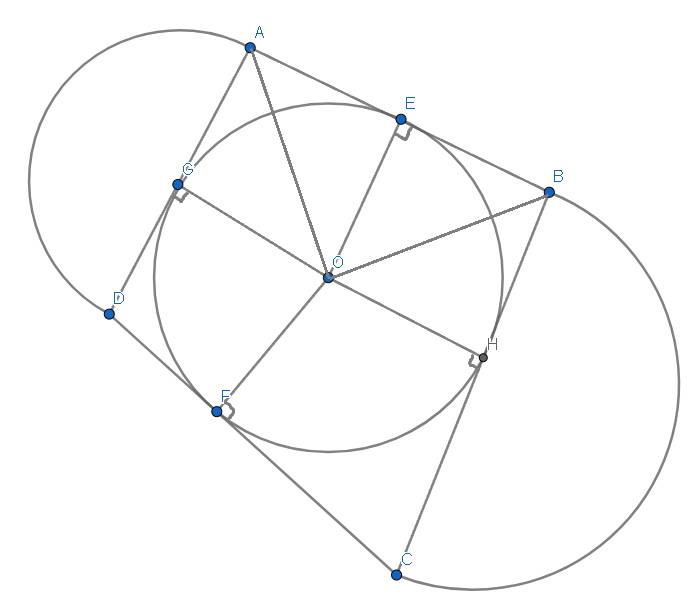
Tứ giác ABCD ngoại tiếp đường tròn (O), vẽ các nửa đường tròn đường kính AD và BC ra phía ngoài của tứ giác. Biết AB + CD = 10cm. Tính tổng các độ dài của hai nửa đường tròn này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB = a; BC = b; CD = c; AD = d
C A B 2 = 2 π . a 2 2 = π . a 2 . Tương tự C C D 2 = π . c 2
Vậy C A B 2 + C C D 2 = π 2 a + c
Có C B C 2 + C C D 2 = π 2 b + d
Tứ giác ABCD ngoại tiếp, kết hợp tính chất tiếp => a + c = b + d => ĐPCM

a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

1. Ta có AD // OM // BC ; OA = OB
=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD
2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi.
3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD
Lại có AD vuông góc với MD => đpcm
4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)
Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB
Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R2 với R = AB/2

a:
ΔABC vuông tại A có AB=AC
nên ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc BDA=1/2*sđ cung BA=90 độ
góc EAC=1/2*sđ cung CA=90 độ
BD vuông góc DA
CE vuông góc AE
mà D,A,E thẳng hàng
nên BD//CE
Xét tứ giác BDEC có
góc BDE+góc DEC+góc DBC+góc ECB=360 độ
=>góc DBC+góc ECB=180 độ
=>góc ECA+góc ACB+góc ABD+góc ABC=180 độ
=>góc ECA+góc ABD=90 độ
góc EAC+góc ECA=90 độ
mà góc DBA+góc ECA=90 độ
nên góc EAC=góc DBA
Xét ΔACE vuông tại E và ΔBAD vuông tại D có
AC=AB
góc EAC=góc DBA
=>ΔACE=ΔBAD
=>AD=CE
b: AD^2+AE^2
=CE^2+AE^2
=AC^2=16
Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π