Tìm số nguyên dương n sao cho n2/(180-n) là số nguyên tố.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
C
0
T
0
QD
0
PT
1
CM
23 tháng 6 2018
Ta có :
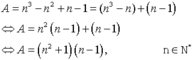
Nếu n = 1 suy ra A = 0
Nếu n = 2 suy ra A = 5 là số nguyên tố
Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số
Vậy để A = n3 – n2 + n – 1 là số nguyên tố thì n = 2.
TK
2
MN
1
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
Lời giải:
Để $p=(n-2)(n^2+n-5)$ là số nguyên tố thì bản thân 1 trong 2 thừa số $n-2, n^2+n-5$ là số nguyên tố và số còn lại bằng 1.
TH1: $n-2=1\Rightarrow n=3$. Khi đó: $p=7$ là số nguyên tố (thỏa mãn)
TH2: $n^2+n-5=1\Rightarrow n^2+n-6=0\Rightarrow (n-2)(n+3)=0$
$\Rightarrow n=2$
$\Rightarrow p=0$ không là snt (loại)
Vậy $n=3$
7 tháng 5 2023
đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
7 tháng 5 2023
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP
QN
3 tháng 3 2018
Đặt \(\frac{n^2}{180-n}\)= P ( P nguyên tố )
=> n2 = P . (180 - n ) => n2 chia hết cho P => n chia hết cho P
=> n = K . P( K thuộc N sao ) thay vào trên ta có :
(K . P)2 = P . ( 180 - K . P )
K2 .P2 = 180 .P - K.P2
K2.P2 +KP2 = 180 .P
K(K + 1) = 180 = 22 . 32 . 5
Do P là số nguyên tố nên P thuộc { 2,3,5}
+> Nếu P = 2 ta có : K .( K+1) =2. 32 . 5 = 90=> K = 90
Khi đó n = 9 .2 =18
+> Nếu P = 3 ta có : K ( K + 1 ) = 22 . 3. 5 = 60 => K thuộc tập hợp rỗng
+> Nếu P = 5 ta có : K ( K +1 ) =22.32 = 36 => K thuộc tập hợp rỗng
Vậy n = 18