Bài 1 Tính Giá Trị Biểu Thức
a) 240x20-(846+202 x2.5)
b)2000 +( 32.4 :3 - 2.8 )
c) 320 x 1.25 - ( 933 + 302 x 3.5 )
Cứu em bài này
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
2
HN
2 tháng 1 2022
a, 2000+(32,4-2,8)x0,25=2000+29,6x0,25
=2000+7,4
=2007,4
b, 97x29+29x2+29=2813+59+29
=2900
c, 200:2x29=100x29
=2900
15 tháng 9 2021
Ta có:
\(A=x\left(x+y\right)-x\left(y-x\right)=x^2+xy-xy+x^2=2x^2\)
Thay \(x=-3\) vào A, ta có:
\(A=2.\left(-3\right)^2=18\)
Vậy A=18
15 tháng 9 2021
\(A=x\left(x+y\right)-x\left(y-x\right)=x\left(x+y\right)+x\left(x+y\right)=\left(x+y\right).2x=\left(-3+2\right).2.\left(-3\right)=6\)
BT
4
19 tháng 12 2023
Câu 1:
\(25\left(x-y\right)^2-16\left(x+y\right)^2\)
\(=\left[5\left(x-y\right)\right]^2-\left[4\left(x+y\right)\right]^2\)
\(=\left(5x-5y\right)^2-\left(4x+4y\right)^2\)
\(=\left(5x-5y-4x-4y\right)\left(5x-5y+4x+4y\right)\)
\(=\left(x-9y\right)\left(9x-y\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-\dfrac{1}{2}\right\}\)
b: \(P=\left(\dfrac{1}{x-1}-\dfrac{x}{1-x^3}\cdot\dfrac{x^2+x+1}{x+1}\right):\dfrac{2x+1}{x^2+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x+1}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+1}{2x+1}=\dfrac{x^2+1}{x^2-1}\)
c: Thay x=1/2 vào P, ta được:
\(P=\dfrac{\left(\dfrac{1}{2}\right)^2+1}{\left(\dfrac{1}{2}\right)^2-1}=\dfrac{5}{4}:\dfrac{-3}{4}=\dfrac{5}{4}\cdot\dfrac{-4}{3}=-\dfrac{5}{3}\)
30 tháng 9 2021
A=\(2^2-9^3+4^{-2}.16-2.5^2\)
\(=4-729+1-50=-774\)
B=\(\left(2^3.2\right).\dfrac{1}{2}+3^{-2}.3^2-7.1+5\)
\(B=2^4.\dfrac{1}{2}+1-7+5=8+1-7+5=7\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8
C = 2-3 + (52)3.5-3 + 4-3.16 - 2.32 - 105.(\(\dfrac{24}{51}\))0
C = \(\dfrac{1}{8}\) + 56.5-3 + 4-3.42 - 2.9 - 105.1
C = \(\dfrac{1}{8}\) + 53 + \(\dfrac{1}{4}\) - 18 - 105
C = (\(\dfrac{1}{8}\) + \(\dfrac{1}{4}\)) - (105 - 125 + 18)
C = \(\dfrac{3}{8}\) - (-20 + 18)
C = \(\dfrac{3}{8}\) + 2
C = \(\dfrac{19}{8}\)
9 tháng 10 2021
A=x(y+2)+2(y+2)=(x+2)(y+2)=100.100=10000
B=9\(^2\)(9+1) +11(-9-1)=\(9^2\).10+11.(-10)=810-110=700
TM
2 tháng 9 2021
a/ \(A=\left(x-1\right)^3-4x\left(x+1\right)\left(x-1\right)+3\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3-3x^2+3x-1-4x^3+4x+3x^3-3\)
\(=-3x^2+7x-4\)
Thay x = 2 vào A được:
\(=-3.2^2+7.2-4=-2\)
Vậy: Giá trị của A khi x = 2 là -2
==========
b/ \(B=126y^3+\left(x-5y\right)\left(x^2+25y^2+5xy\right)\)
\(=126y^3+x^3-125y^3\)
Thay x = -5 và y = -3 vào B được:
\(126.\left(-3\right)^3+\left(-5\right)^3-125.\left(-3\right)^3=-152\)
Vậy: Giá trị của B tại x = -5 và y = -3 là -152
==========
c/ \(C=a^3+b^3-\left(a^2-2ab+b^2\right)\left(a-b\right)\)
\(=a^3+b^3-\left(a-b\right)^3\)
\(=a^3+b^3-a^3+3a^2b-3ab^2+b^3\)
\(=2b^3+3a^2b-3ab^2\)
Thay a = -4 và b = 4 vào C được:
\(2.4^3+3.\left(-4\right)^2.4-3.\left(-4\right).4^2=512\)
Vậy: Giá trị của C tại a = -4 vào b = 4 là 512
2 tháng 9 2021
a:Ta có: \(A=\left(x-1\right)^3-4x\left(x+1\right)\left(x-1\right)+3\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3-3x^2+3x-1-4x^3+4x+3x^3-3\)
\(=-3x^2+7x-4\)
\(=-3\cdot2^2+7\cdot2-4\)
\(=-12-4+14=-2\)
c: Ta có: \(C=a^3+b^3-\left(a-b\right)\left(a^2-2ab+b^2\right)\)
\(=a^3+b^3-a^3+3a^2b-3ab^2+b^3\)
\(=2b^3+3a^2b-3ab^2\)
\(=2\cdot4^3+3\cdot\left(-4\right)^2\cdot4-3\cdot\left(-4\right)\cdot4^2\)
\(=128+192+192=512\)
9 tháng 7 2021
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
9 tháng 7 2021
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
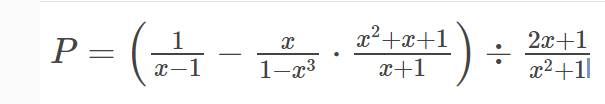
a/\(240\times20-\left(846+202\times2,5\right)\)
\(=4800-\left(846+505\right)\)
\(=4800-1351\)
\(=3449\)
b/\(2000+\left(32,4:3-2,8\right)\)
\(=2000+\left(10,8-2,8\right)\)
\(=2000+8\)
\(=2008\)
c/\(320\times1,25-\left(933+302\times3,5\right)\)
\(=400-\left(933+1057\right)\)
\(=400-1990\)
\(=-1590\)
cảm ơn ạ