cho tam giác ABC vuông tại A (AC>AB) trên AC lấy 1 điểm N và vẽ đường tròn đường kính NC . kẻ BN cắt đường tròn tại K .đường thẳng KA cắt đường tròn tại H .chứng minh rằng
a) ABCK là tứ giác nội tiếp
b)góc ABK=ACK
c)CA là tia phân giác của HCB
d) biết bán kính của đường tròn là R và GÓC ACB =30 độ . tính độ dài cung nhỏ NH theo R

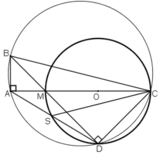
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
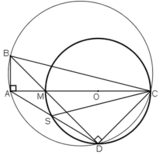
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
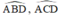 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 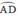
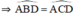
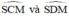 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 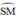
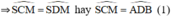
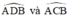 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 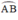
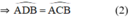

giúp câu d nha