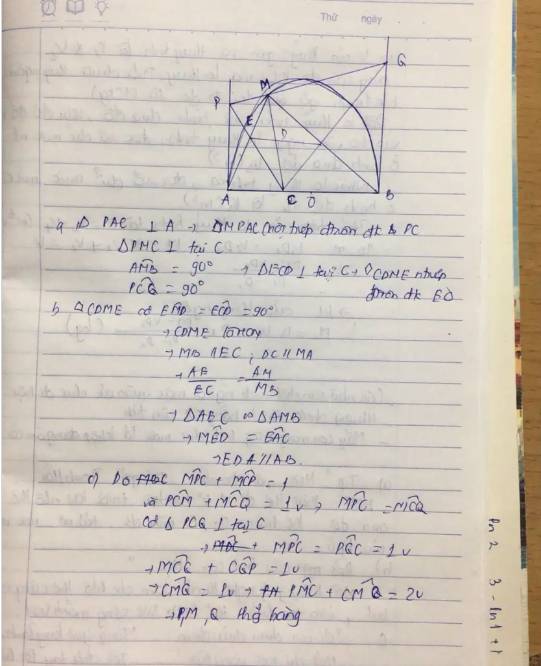
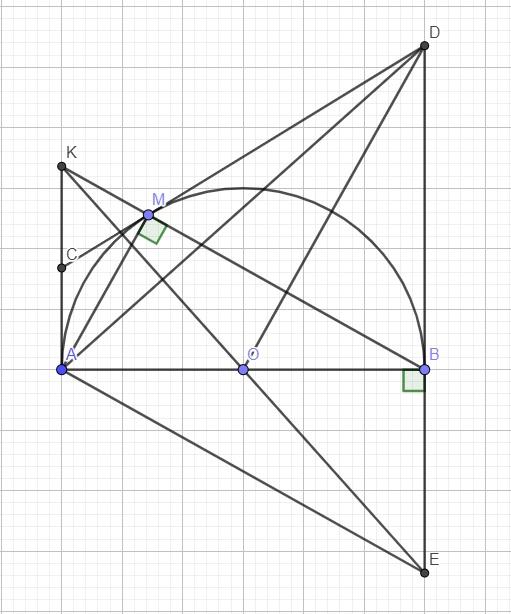
cho nửa dg tròn (O) dg kính AB . trên nửa dg tròn lấy điểm M . trên AB lấy điểm C sao cho AC,<CB . Gọi Ax,By là 2 tiếp tuyến của nửa đường tròn.đường thẳng đi qua M và vg mới MC cắt Ax ờ P, đường thẳng qua C và vg với CP cắt By tại Q Gọi D là gd của CP và AM ;E là giao điểm của CQ với BM
a)chứng minh AB//DE
B)chứng minh M,P,Q thẳng hàng