Cho hình vẽ sau: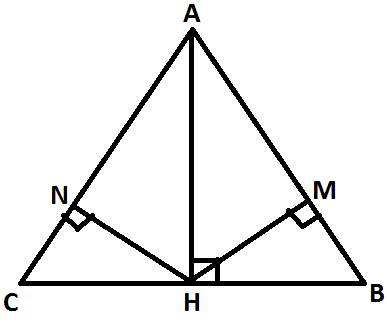
Cho Å1 =Å2
MN⊥AC
HM⊥AB
a, CM ΔAHC=ΔAHB
b, CM ΔHNC=ΔHMB
mọi người giải giúp mình với, mình c.ơn trước ạ:33
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không có cái hình thì có biết hình dạng nó ra sao đâu mà giúp được bạn ơi?

a: Xét ΔANH vuông tại N và ΔAHB vuông tại H có
góc NAH chung
=>ΔANH đồng dạng với ΔAHB
b: ΔAHC vuông tại H có HM là đường cao
nên AM*AC=AH^2
ΔAHB vuông tại H có HN là đường cao
nên AN*AB=AH^2
=>AM*AC=AN*AB
=>AM/AB=AN/AC
c: AM/AB=AN/AC
=>ΔAMN đồng dạng với ΔABC
=>góc AMN=góc ABC
=>góc NMC+góc NBC=180 độ
=>BNMC là tứ giác nội tiếp
=>góc INB=góc ICM
Xét ΔINB và ΔICM có
góc INB=góc ICM
góc I chung
=>ΔINB đồng dạng với ΔICM
=>IN/IC=IB/IM
=>IN*IM=IB*IC

xet tg AMH vuong tai M co; AH2 = AM2 + HM2
tg BMH co; BM2 = BH2-HN2
cong 2 pt ban toi da nhan ra chua ban co thay AM=AN ; HM = HN thay vao ban se thay phep dieu ky
ma toi mang den cho ban la dpcm

Bài 1:
ΔDMK vuông tại M
=>\(DM^2+MK^2=DK^2\)
=>\(DM^2=12^2-10^2=44\)
=>\(DM=2\sqrt{11}\left(cm\right)\)
ΔDMN vuông tại D
=>\(DM^2+DN^2=MN^2\)
=>\(DN^2+44=324\)
=>\(DN^2=280\)
=>\(DN=2\sqrt{70}\left(cm\right)\)
Bài 2:
ΔGNH vuông tại G
=>\(GN^2+GH^2=HN^2\)
=>\(HN^2=8^2+12^2=208\)
=>\(HN=4\sqrt{13}\left(cm\right)\)
Xét ΔGNH vuông tại G có \(cosGNH=\dfrac{GN}{HN}=\dfrac{2}{\sqrt{13}}\)
=>\(cosNHM=\dfrac{2}{\sqrt{13}}\left(\widehat{GNH}=\widehat{NHM}\right)\) do GN//HM
Xét ΔNHM có \(cosNHM=\dfrac{HN^2+HM^2-NM^2}{2\cdot HN\cdot HM}\)
=>\(\dfrac{52+HM^2-484}{2\cdot4\sqrt{13}\cdot HM}=\dfrac{2}{\sqrt{13}}\)
=>\(HM^2-432=\dfrac{2}{\sqrt{13}}\cdot2\cdot4\sqrt{13}\cdot HM\)
=>\(HM^2-432=16HM\)
=>\(HM^2-16HM-432=0\)
=>\(\left[{}\begin{matrix}HM=8+4\sqrt{31}\left(cm\right)\left(nhận\right)\\HM=8-4\sqrt{31}\left(loại\right)\end{matrix}\right.\)

a) vì M là tđ AB -> AM=1/2AB=5cm
N là tđ AC -> AN=1/2AC= 12cm
áp dụng pytago vào tam giác ANM => MN=13cm
b) theo công thức tính diện tích tam giác ANM (cái này mình chưa biết bạn học chưa, nếu chưa thì nhắn cho mình giải thích cho)
1/2(AM x AN) = 1/2(MN x AH)
=> AM x AN = MN x AH -> 5 x 12 = 13 x AH
=> AH=60/13cm
c) xét 2 tam giác BKM vuông tại K và AHM vuông tại H
có góc AMH + góc BMK ( đối đỉnh )
AM=MB ( M là Tđ AB)
=> 2 tam giác BKM=AHM (cạnh huyền góc nhọn)
d) áp dụng pytago vào tam giác AHM vuông tại H
AM2-AH2=HM2 => HM=MK=25/13cm (vì 2 tam giác ở câu c bằng nhau)
tam giác ABC có góc A vuông
ta có : BC2 = AB2 +AC2 ( định lý pytago )
thay BC2 = 102 + 242
=> BC=26 cm
ta lại có : M là trung điểm của AB => AM=1/2AB=1/2 . 10 =5 cm
tương tự : N là trung điểm của AC => AN = 1/2AC = 1/2 .24 = 12 cm
tam giác AMN vuông tại A , ta có : MN2 = AM2 + AN2 ( định lí pytago )
thay MN2 = 52 + 122
=> MN = 13 cm
Vậy MN = 13 cm
Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)
`MN` ở đâu vậy ạ?