Tìm x, y, z biết: (x - y2 + z)2 + (y - 2)2 + (z + 3)2 = 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
<=> \(\hept{\begin{cases}\left(x-y^2+z\right)^2=0\\\left(y-2\right)^2=0\\\left(z+3\right)^2=0\end{cases}}\) <=> \(\hept{\begin{cases}\left(x-2^2-3\right)^2=0\\y=2\\z=-3\end{cases}}\) <=> \(\hept{\begin{cases}x=7\\y=2\\z=-3\end{cases}}\)
Câu 4 tương tự.

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
$A\geq \frac{9}{x+2+y+2+z+2}=\frac{9}{x+y+z+6}$
Áp dụng BĐT Bunhiacopxky:
$(x^2+y^2+z^2)(1+1+1)\geq (x+y+z)^2$
$\Rightarrow 9\geq (x+y+z)^2\Rightarrow x+y+z\leq 3$
$\Rightarrow A\geq \frac{9}{x+y+z+6}\geq \frac{9}{3+6}=1$
Vậy $A_{\min}=1$. Dấu "=" xảy ra khi $x=y=z=1$

Lời giải:
Ta thấy:
$(-x^2y^3)^2\geq 0$ với mọi $x,y$
$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$
$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:
$-x^2y^3=2y^2z^4=0$
Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.

Lời giải:
Vì $x+y+z=0\Rightarrow x=-(y+z)$
$\Rightarrow x^2=(y+z)^2$
$\Rightarrow \frac{x^2}{x^2-y^2-z^2}=\frac{x^2}{(y+z)^2-y^2-z^2}=\frac{x^2}{2yz}=\frac{x^3}{2xyz}$
Hoàn toàn tương tự với các phân thức còn lại:
\(\frac{x^2}{x^2-y^2-z^2}+\frac{y^2}{y^2-z^2-x^2}+\frac{z^2}{z^2-x^2-y^2}=\frac{x^3+y^3+z^3}{2xyz}=\frac{(x+y)^3-3xy(x+y)+z^3}{2xyz}\)
\(=\frac{(-z)^3-3xy(-z)+z^3}{2xyz}=\frac{3xyz}{2xyz}=\frac{3}{2}\)
Năng Cộng Nguyễn: bạn lưu ý lần sau gõ đề bằng công thức toán.

\(\Rightarrow\)x-y^2+z=0
y-2=0
z+3=0
\(\Rightarrow\)\(\hept{\begin{cases}x-4-3=0\\y=2\\z=-3\end{cases}}\)x=7


Mỗi hạng tử của đa thức đều không âm, do đó tổng của chúng không âm. Tổng của chúng bằng 0, do đó mỗi hạng tử bằng 0.
\(\Rightarrow\hept{\begin{cases}x-y^2+z=0\\y-2=0\\z+3=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=y^2-z=7\\y=2\\z=-3\end{cases}}}\)
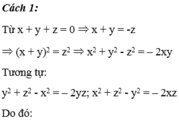
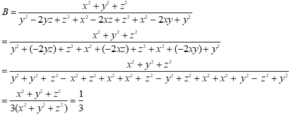
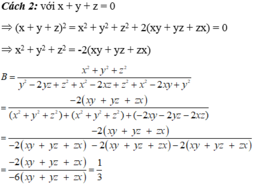
ta có : ( x - y2 + z) 2 > 0 , mọi x,y,z
(y-2) 2 >0 , mọi y
( x+3 ) >0 , mọi x
=> x= -5 ; z= -3 ; y=-2