Trong mặt phẳng tọa độ lấy các điểm A(0;6), B(6;0) và C(1;1). Diện tích tam giác ABC là ............ (đvđd)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình mặt chắn của mặt phẳng (ABC) là: ![]()
Từ giả thiết 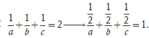 Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.

Đáp án A.
6 x - 3 y + 2 z - 12 = 0 .
Tương tự
B 0 ; 4 ; 0 , C 0 ; 0 ; 6 ⇒ A B C : x 2 + y 4 + z 6 = 1 ⇔ 6 x + 3 y + 2 z − 12 = 0.

Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.

Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
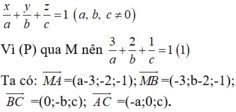
Vì M là trực tâm của tam giác ABC nên:
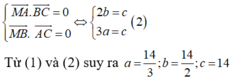
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
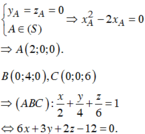
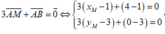
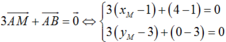
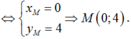



Lấy D(0;1) và E(1;0)
Ta thấy ngay \(S_{ABC}=S_{AOB}-S_{ADC}-S_{BCE}-S_{DCEO}\)
\(S_{AOB}=\frac{1}{2}.6.6=18\)
\(S_{ACD}=S_{BCE}=\frac{1}{2}.1.5=2,5\)
\(S_{DCEO}=1\)
Vậy thi \(S_{ABC}=18-2.2,5-1=12\left(đvdt\right)\)
Có công thức mà bạn