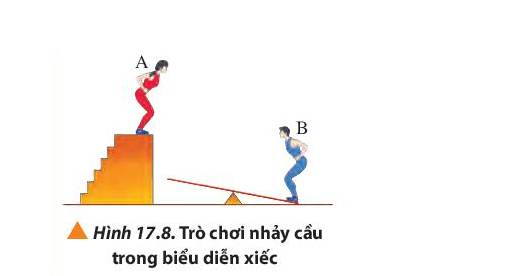
Thảo luận và chỉ ra các dạng năng lượng của hai vận động viên xiếc khi thực hiện trò chơi nhảy cầu (Hình 17.8) vào lúc:
a) Người A chuẩn bị nhảy, người B đứng trên đòn bẩy.
b) Người A chạm vào đòn bẩy.
c) Người B ở vị trí cao nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Người A có dạng năng lượng là thế năng, người B có động năng
b) Người A chạm vào đòn bẩy thì A có động năng
c) Người B ở vị trí cao nhất thì B có thể năng.

Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Chọn hệ trục tọa độ Oxy như hình dưới:
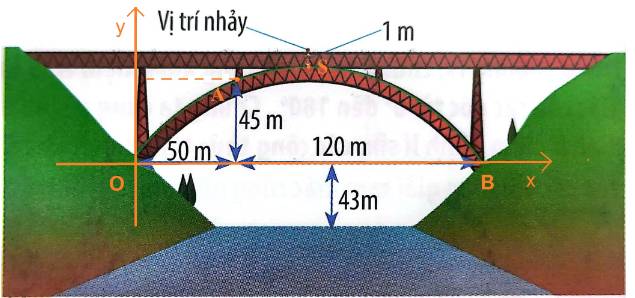
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)

Khi vận động viên chạm mặt nước nghĩa là h = 0m
Ta có: 0 = - x - 1 2 + 4 ⇔ x 2 -2x -3 =0
∆ ' = b ' 2 – ac = - 1 2 -1.(-3) =1 +3 = 4 > 0
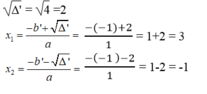
Vì khoảng cách không thể mang giá trị âm nên x=3m

Cơ năng:
\(W=W_đ+W_t\)
\(\Rightarrow W=\dfrac{1}{2}mv_0^2+mgh\)
\(\Rightarrow W=\dfrac{1}{2}\cdot\dfrac{650}{10}\cdot2^2+\dfrac{650}{10}\cdot10\cdot10=6630J\)
Khi chạm nước:
\(W=W'=\dfrac{1}{2}mv'^2=\dfrac{1}{2}\cdot\dfrac{650}{10}\cdot v'^2=6630\)
\(\Rightarrow v'=2\sqrt{51}\)m/s

đang đứng ở 4 gọc phòng và khi chạm tay lại là góc phòng bên cạnh chứ không phải cùng phòng nữa
Người A đến chạm vào B rồi đứng ở chỗ người B, tiếp theo người B di chuyển đến chỗ người C và thế chỗ C, rồi người C thế chỗ người D, người D đến chạm vào người A và thế chỗ người A, lần lượt là như vậy cho đến sáng. Nhưng chẳng phải A đang đứng ở chỗ B rồi đấy sao? Vậy thì đáng lẽ sẽ không có ai ở đó mới phải chứ? Vậy cái người thứ 5 đứng sẵn ở vị trí A để người D đến chạm vào và thế chỗ đó là ai trong khi chỉ có 4 cậu sinh viên trong phòng với nhau? MA!

Trả lời :
Chỉ có 4 người chơi nhưng trò chơi này yêu cầu phải có 5 người mới có thể lần lượt thay phiên nhau đến đụng từng người vì nếu thiếu 1 người, 1 vị trí sẽ trống. Người A đến thế chỗ người B, người C thế chỗ người D, người D đến chỗ người A thì đáng lẽ sẽ không có ai ở đó mới phải? Vậy người thứ 5 là ai?
Lời giải: Chỉ có 4 người chơi nhưng trò chơi này yêu cầu phải có 5 người mới có thể lần lượt thay phiên nhau đến đụng từng người vì nếu thiếu 1 người, 1 vị trí sẽ trống. Người A đến thế chỗ người B, người C thế chỗ người D, người D đến chỗ người A thì đáng lẽ sẽ không có ai ở đó mới phải? Vậy người thứ 5 là ai? là ma chứ ai

Khi vận động viên ở độ cao 3m nghĩa là h =3m
Ta có: 3 = - x - 1 2 + 4 ⇔ x - 1 2 – 1=0 ⇔ x 2 – 2x = 0
⇔ x(x – 2) = 0 ⇔ x=0 hoặc x – 2 =0 ⇔ x = 0 hoặc x = 2
Vậy x = 0m hoặc x = 2m
a) Người A có dạng năng lượng là thế năng, người B có động năng
b) Người A chạm vào đòn bẩy thì A có động năng
c) Người B ở vị trí cao nhất thì B có thể năng.