Cho mạch điện , biết r1=4 , r2=8 , r3=12 , rx là 1 biến trở . Hiệu điện thế giữa hai đầu dây dẫn AB luôn được duy trì 20v . A. Tính công suất tỏa nhiệt của mạch AB khi rx =6 . B. Nối c với d bằng 1 dây dẫn có điện trở không đáng kể . Người ta đo được dòng điện chạy qua r2 có cường độ 1.8A . Hãy tính giá trị rx tham gia vào mạch điện đó .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
10 tháng 2 2019
a) Tìm công suất tỏa nhiệt trên điện trở R 4
Chọn chiều dòng điện qua các điện trở trong mạch như hình vẽ.
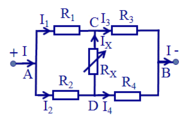
* Xét tại nút A ta có: I = I 1 + I 2 (1)
Với vòng kín ACDA ta có:
I 1 R 1 - I X R X - I 2 R 2 = 0 (2)
Thế (1) vào (2) ta được biểu thức I :
I 1 R 1 - I X R X - ( I - I 1 ) R 2 = 0 I 1 R 1 - I X R X - I R 2 + I 1 R 2 = 0 I 1 ( R 1 + R 2 ) = I X R X + I R 2 ⇒ I 1 = I X . R X + I . R 2 R 1 + R 2 = I X . R X + I . R 4 R (3)
* Xét tại nút B ta có: I 3 = I - I 4 (4)
Với vòng kín BCDB ta có:
I 3 R 3 - I X R X + I 4 R 4 = 0 I 3 R - I X R X + I 4 X = 0 (5)
Thế (4) vào (5) ta có biểu thức
I
4
:
(
I
-
I
4
)
R
-
I
X
R
X
+
I
4
R
=
0
I
.
R
+
I
4
R
-
I
X
R
X
+
I
4
R
=
0
⇒ I 4 = I . R + I X R X 2 R (6)
Từ (3) và (6) ta có: = 2 ð = =
Vậy công suất tỏa nhiệt trên R 4 khi đó là P 4 = 4 3 P 1 = 12 W .
b) Tìm R X theo R để công suất tỏa nhiệt trên R X cực đại
Từ (4) và (5) ta có biểu thức I 3 :
I 3 R - I X R X + ( I - I 3 ) R = 0 I 3 R - I X R X + I R - I 3 R = 0 ⇒ I 3 = I . R - I X R X 2 R (7)
Ta có: U = U A B = U A C + U C B = I 1 . R 1 + I 3 R 3 U = I 1 3 R + I 3 R (8)
Thế (3) và (7) vào (8) ta được:
U = I X R X + I . R 4 R . 3 R + I . R - I X R X 2 R . R 4 U = 3 . I X R X + 3 . I . R + 2 I . R - 2 I X R X 4 U = 5 . I . R + I X R X (9)
Tính I:
Ta có:
I = I 1 + I 2 = I 1 + I 4 + I X = 3 I 1 + I X = 3 . I X R X + I R 4 R + I X ⇒ 4 . I . R = 3 I X R X + 3 . I . R + 4 . I X . R ⇒ I R = 3 I X . R X + 4 . I X . R t h a y v à o ( 9 ) t a đ ư ợ c : 4 U = 5 . ( 3 I X . R X + 4 I X . R ) + I X R X = 15 . I X . R X + 20 I X R + I X R X = 16 . I X R X + 20 I X R ⇒ I X = U 4 R X + 5 R
Hai số dương 4 R x và 5 R R x có tích 4 R x . 5 R R x = 20 R không đổi thì theo bất đẳng thức Côsi, tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau nghĩa là khi 4 R x = 5 R R x ⇒ R x = 1 , 25 R ; mẫu số ở vế phải của biểu thức (10) nhỏ nhất nghĩa là P X cực đại. Vậy PX cực đại khi R X = 1 , 25 R .
6 tháng 11 2018
Bài 1 :
Tóm tắt :
\(R_1=6\Omega\)
\(R_2=30\Omega\)
\(R_3=15\Omega\)
U = 24V
______________________
\(I_2=?\)
GIẢI :
Ta có : R1nt(R2//R3)
Nên: Điện trở tương đương toàn mạch là :
\(R_{tđ}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=6+\dfrac{30.15}{30+15}=16\left(\Omega\right)\)
=> \(I=\dfrac{U}{R_{tđ}}=\dfrac{24}{16}=1,5\left(A\right)\)
=> I = I1 =I23 =1,5A ; \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{30.15}{30+15}=10\left(\Omega\right)\)
Hiệu điện thế U23 là :
\(U_{23}=I_{23}.R_{23}=1,5.10=15\left(V\right)\)
Vì R2//R3 => U2=U3= U23 = 15V
Cường độ dòng điện chạy qua điện trở R2 là :
\(I_2=\dfrac{U_2}{R_2}=\dfrac{15}{30}=0,5\left(A\right)\)
Vậy cường độ dòng điện chạy qua điện trở R2 có độ lớn là 0,5A
27 tháng 12 2022
a)\(R_1ntR_2\Rightarrow R_{12}=R_1+R_2=15+12=27\Omega\)
\(I=\dfrac{U}{R}=\dfrac{18}{27}=\dfrac{2}{3}A\)
Công suất toả nhiệt: \(P=U\cdot I=RI^2=27\cdot\left(\dfrac{2}{3}\right)^2=12W\)
b)\(R_3//\left(R_1ntR_2\right)\Rightarrow R_{tđ}=\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}\)
\(P_{AB}=24W\Rightarrow R_{tđ}=\dfrac{U^2}{P}=\dfrac{18^2}{24}=13,5\Omega\)
\(\Rightarrow\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}=13,5\Rightarrow\dfrac{27\cdot R_3}{27+R_3}=13,5\)
\(\Rightarrow R_3=27\Omega\)
DM
4 tháng 11 2017
a) Điện trở tương đương toàn mạch :
\(R_{tđ}=R_1+\dfrac{R_2\cdot R_3}{R_2+R_3}=10+\dfrac{20\cdot60}{20+60}=10+15=25\left(\Omega\right)\)
Cường độ dòng điện qua điện trở \(R_1\):
\(I_C=I_1=\dfrac{U}{R_{tđ}}=\dfrac{12}{25}=0,48\left(A\right)\)
Hiệu điện thế 2 đầu \(R_1\)
\(U_1=I_1\cdot R_1=0,48\cdot10=4,8\left(V\right)\)
Hiệu điện thế của đoạn mạch song song :
\(U_{//}=U-U_1=12-4,8=7,2\left(V\right)\)
Cường độ dòng điện qua điện trở R2,R3 :
\(I_2=\dfrac{U_{//}}{R_2}=\dfrac{7,2}{20}=0,36\left(A\right)\)
\(I_3=\dfrac{U_{//}}{R_3}=\dfrac{7,2}{60}=0,12\left(A\right)\)
Công suất tỏa nhiệt trên toàn mạch :
\(P=UI_C=12\cdot0,48=5,76\left(W\right)\)
b) Theo đề ta có :
\(I_C'=\dfrac{U}{R_{tđ}'}\Leftrightarrow0,5=\dfrac{12}{R_X+\dfrac{R_1R_2}{R_1+R_2}}\Leftrightarrow0,5=\dfrac{12}{R_X+15}\)
Giải tìm \(R_X\) được \(R_X=9\left(\Omega\right)\)
Vậy giá trị \(R_X=9\left(\Omega\right)\).