Cho tam giác ABC có góc B,c là các góc nhọn. Đường cao AH và trung tuyến AM biết góc BAH = góc MAC.
a) Gọi E là trung điểm của AB. CMr AEHM là tứ giác nội tiếp.
b) Tính góc BAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2018
Bạn ơi xem lại đề đi nha , ko có đường tròn sao lại có đường kính AH
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
a.
Do E là trung điểm AB, M là trung điểm BC
\(\Rightarrow\) EM là đường trung bình tam giác ABC
\(\Rightarrow EM||AC\)
\(\Rightarrow\widehat{MAC}=\widehat{AME}\) (so le trong) (1)
Trong tam giác vuông AHB, HE là trung tuyến ứng với cạnh huyền
\(\Rightarrow HE=\dfrac{1}{2}AB=AE\) \(\Rightarrow\Delta AHE\) cân tại E
\(\Rightarrow\widehat{AHE}=\widehat{BAH}\) (2)
Mà \(\widehat{BAH}=\widehat{MAC}\) (giả thiết) (3)
(1);(2);(3) \(\Rightarrow\widehat{AME}=\widehat{AHE}\)
\(\Rightarrow AMHE\) nội tiếp (2 góc bằng nhau cùng chắn AE)
\(\Rightarrow\) 4 điểm A, E, M, H cùng thuộc 1 đường tròn
b.
Theo cmt AMHE nội tiếp \(\Rightarrow\widehat{AEM}=\widehat{AHM}=90^0\) (cùng chắn AM)
\(\Rightarrow EM\perp AB\)
Mà \(EM||AC\)
\(\Rightarrow AB\perp AC\)
\(\Rightarrow\widehat{BAC}=90^0\)
7 tháng 3 2016
goi goc BAH,MAH,MAC là A1, A2 ,A3 ta co;
B+A1 = 90 mà A1=A2=A3
nen BAC=90
lam k met viet met qua
5 tháng 7 2023
a: góc ACM=1/2*sđ cung AM=90 độ
b: góc ADB=góc AEB=90 độ
=>ABDE nội tiếp
24 tháng 11 2023
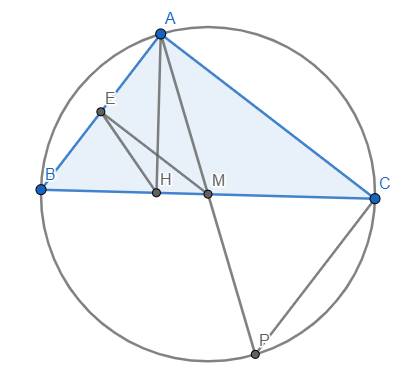
a) Gọi P là giao điểm của AM với (O). Tam giác ABH và APC có:
\(\widehat{BAH}=\widehat{PAC}\left(gt\right)\) và \(\widehat{ABH}=\widehat{APC}\) (góc nội tiếp cùng chắn cung AC)
\(\Rightarrow\Delta ABH~\Delta APC\left(g.g\right)\) \(\Rightarrow\widehat{AHB}=\widehat{ACP}\).
Mà \(\widehat{AHB}=90^o\Rightarrow\widehat{ACP}=90^o\) . Suy ra M nằm trên đường kính AP của (O).
Mặt khác, M lại là trung điểm của dây BC của (O), do đó nếu dây BC không phải là đường kính của (O) thì phải có \(AP\perp BC\) , điều này không chắc chắn đúng. Do đó để đảm bảo M là trung điểm BC thì BC phải là đường kính của (O).
\(\Rightarrow\) M là tâm của (O). Từ đó \(\widehat{MBA}=\widehat{MAB}\)
Trong tam giác HAB vuông tại H có trung tuyến HE nên \(EH=EA=EB=\dfrac{AB}{2}\), do đó \(\widehat{ABM}=\widehat{EHB}\).
Từ đó suy ra \(\widehat{MAB}=\widehat{EHB}\) \(\Rightarrow\) Tứ giác AMHE nội tiếp (đpcm)
b) Từ câu a), ta có BC là đường kính của (O) nên suy ra đpcm.