Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi xem lại đề đi nha , ko có đường tròn sao lại có đường kính AH

a.
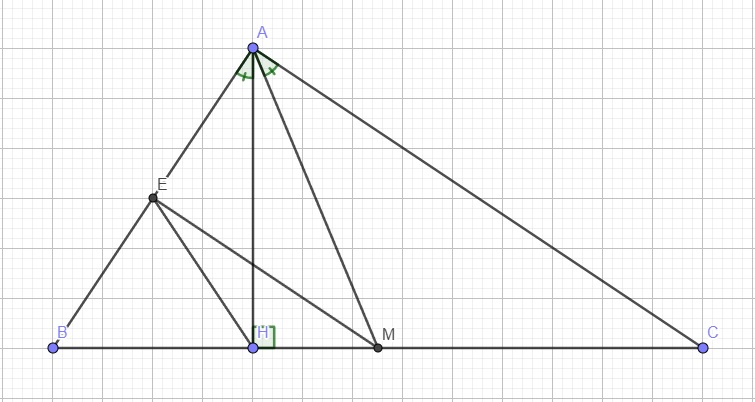
Do E là trung điểm AB, M là trung điểm BC
\(\Rightarrow\) EM là đường trung bình tam giác ABC
\(\Rightarrow EM||AC\)
\(\Rightarrow\widehat{MAC}=\widehat{AME}\) (so le trong) (1)
Trong tam giác vuông AHB, HE là trung tuyến ứng với cạnh huyền
\(\Rightarrow HE=\dfrac{1}{2}AB=AE\) \(\Rightarrow\Delta AHE\) cân tại E
\(\Rightarrow\widehat{AHE}=\widehat{BAH}\) (2)
Mà \(\widehat{BAH}=\widehat{MAC}\) (giả thiết) (3)
(1);(2);(3) \(\Rightarrow\widehat{AME}=\widehat{AHE}\)
\(\Rightarrow AMHE\) nội tiếp (2 góc bằng nhau cùng chắn AE)
\(\Rightarrow\) 4 điểm A, E, M, H cùng thuộc 1 đường tròn
b.
Theo cmt AMHE nội tiếp \(\Rightarrow\widehat{AEM}=\widehat{AHM}=90^0\) (cùng chắn AM)
\(\Rightarrow EM\perp AB\)
Mà \(EM||AC\)
\(\Rightarrow AB\perp AC\)
\(\Rightarrow\widehat{BAC}=90^0\)

goi goc BAH,MAH,MAC là A1, A2 ,A3 ta co;
B+A1 = 90 mà A1=A2=A3
nen BAC=90
lam k met viet met qua

a: góc ACM=1/2*sđ cung AM=90 độ
b: góc ADB=góc AEB=90 độ
=>ABDE nội tiếp

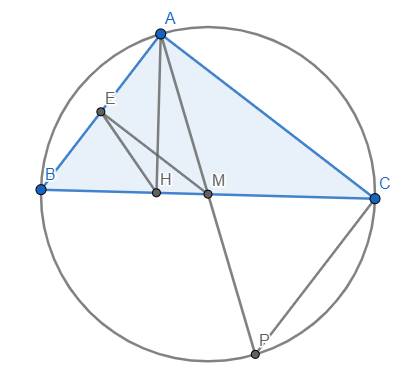
a) Gọi P là giao điểm của AM với (O). Tam giác ABH và APC có:
\(\widehat{BAH}=\widehat{PAC}\left(gt\right)\) và \(\widehat{ABH}=\widehat{APC}\) (góc nội tiếp cùng chắn cung AC)
\(\Rightarrow\Delta ABH~\Delta APC\left(g.g\right)\) \(\Rightarrow\widehat{AHB}=\widehat{ACP}\).
Mà \(\widehat{AHB}=90^o\Rightarrow\widehat{ACP}=90^o\) . Suy ra M nằm trên đường kính AP của (O).
Mặt khác, M lại là trung điểm của dây BC của (O), do đó nếu dây BC không phải là đường kính của (O) thì phải có \(AP\perp BC\) , điều này không chắc chắn đúng. Do đó để đảm bảo M là trung điểm BC thì BC phải là đường kính của (O).
\(\Rightarrow\) M là tâm của (O). Từ đó \(\widehat{MBA}=\widehat{MAB}\)
Trong tam giác HAB vuông tại H có trung tuyến HE nên \(EH=EA=EB=\dfrac{AB}{2}\), do đó \(\widehat{ABM}=\widehat{EHB}\).
Từ đó suy ra \(\widehat{MAB}=\widehat{EHB}\) \(\Rightarrow\) Tứ giác AMHE nội tiếp (đpcm)
b) Từ câu a), ta có BC là đường kính của (O) nên suy ra đpcm.

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\left(1\right)\)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAB}+\widehat{ABH}=90^0\)(ΔABH vuông tại H)
Do đó: \(\widehat{ACB}=\widehat{HAB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAC}=\widehat{HAB}\)
c: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AFE}=\widehat{ABC}\)
\(\widehat{AFE}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>FE vuông góc AM tại K
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HA^2=AE\cdot AB\)
=>\(AE\cdot6=4,8^2\)
=>\(AE=3,84\left(cm\right)\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{4.8^2}{8}=2,88\left(cm\right)\)
Xét ΔAEF vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
=>\(\dfrac{1}{AK^2}=\dfrac{1}{2,88^2}+\dfrac{1}{3.84^2}\)
=>AK=2,304(cm)