Bài 4: Trên tia Ox vẽ các điểm M1; M2; M3. Nếu trong mặt phẳng chứa tia Ox vẽ thêm
các điểm M4; M5; M6; ...; M101; M102. Trong các điểm M1; M2; M3; ...; M101; M102có đúng 3
điểm thẳng hàng và cứ qua hai điểm ta vẽ được một đường thẳng. Có tất cả bao nhiêu
đường thẳng như thế? Tại sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 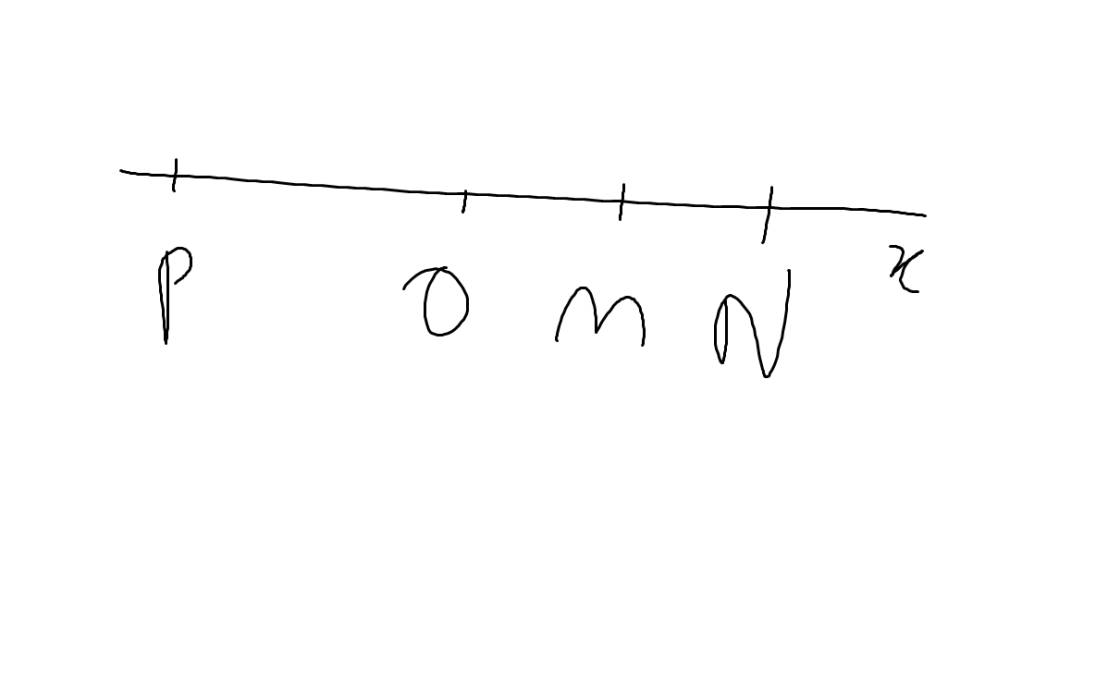
b: ON=2*OM=2*4=8cm
Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN=8-4=4cm
OP và ON là hai tia đối nhau
=>O nằm giữa P và N
=>PN=PO+ON=8+8=16(cm)
c: Vì O nằm giữa P và N
và OP=ON
nên O là trung điểm của PN
Ta có: M nằm giữa O và N
MO=MN
Do đó: M là trung điểm của ON

bài 1\
qua 2 điểm ta vẽ được 1 đường thẳng.
chọn 1 điểm bất kì trong n điểm. qua điểm đó và (n-1) điểm còn lại ta có (n-1) đường thẳng. làm như vậy với n điểm thì về được n.(n-1) duông thắng. nhưng như vậy số đường thẳng đã được tính 2 lần nên thực chất số đường thẳng có là n.(n-1):2=435 đường thẳng
suy ra n.(n-1)=435x2
n.(n-1)=870
n.(n-1)=30x29
suy ra n=30
vay có 30 diểm
Lấy 1 điểm trong n điểm đã cho nối với n-1 điểm còn lại ta được n-1 đường thẳng.
Làm như vậy với n điểm ta được: n(n-1) đường thẳng.
Mà mỗi đường thẳng được tính 2 lần.
=> Số đường thẳng thực tế là: \(\frac{n\left(n-1\right)}{2}\)
Mà có 435 đường thẳng tạo thành.
=> \(\frac{n\left(n-1\right)}{2}\)= 435
n(n-1) = 870.
Mà 870=30.29
=> n=30