 giúp mình bài 3
giúp mình bài 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tiêu đề bài hai có nghĩa là j zậy bnnnnnnnnnnnnnnnn
mk nhát đọc đề quá

2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)

1,Áp dụng định lý Pi-ta-go vào tam giác vuông AHB ta có:
\(AH^2+BH^2+AB^2\\
\Rightarrow x^2+4^2=\sqrt{52^2}\\
\Rightarrow x^2+16=52\\
\Rightarrow x^2=36\\
\Rightarrow x=6\left(vì.x>0\right)\)
Áp dụng định lý Pi-ta-go vào tam giác vuông AHC ta có:
\(AH^2+HC^2=AC^2\\ \Rightarrow6^2+9^2=y^2\\ \Rightarrow36+81=y^2\\ \Rightarrow117=y^2\\ \Rightarrow y=\sqrt{117}\left(vì.y>0\right)\)
2,Ta có BC=BH+HC=4+9=13
Ta có:\(AB^2+AC^2=\sqrt{52^2}+\sqrt{117^2}=52+117=169\)
\(BC^2=13^2=169\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pt-ta-go đảo)
a. Áp dụng định lý pitago vào tam giác vuông ABH
\(AB^2=AH^2+BH^2\)
\(\Rightarrow x=\sqrt{AB^2-BH^2}=\sqrt{\sqrt{52^2}-4^2}=\sqrt{52-16}=\sqrt{36}=6cm\)
Áp dụng định lý pitago vào tam giác vuông ACH
\(AC^2=AH^2+HC^2\)
\(\Rightarrow y=\sqrt{6^2+9^2}=\sqrt{117}=3\sqrt{13}\)
b. ta có: BC = 13 cm
AB = \(\sqrt{52}cm\)
\(AC=\sqrt{117}cm\)
Ta có: \(BC^2=AB^2+AC^2\)
\(13^2=\sqrt{52^2}+\sqrt{117^2}\)
\(169=169\) ( đúng )
Vậy tam giác ABC là tam giác vuông ( pitago đảo ) và vuông tại A

bài 3 A) 17:(34:100)=........%
B) số học sinh nữ là
35-17=18 bạn
tỉ số % là
18:17x100=..............%
Bài 5) số thứ 2 là
93,26-67,9=25,36
số thứ 1 là
67,9-25,36= 42,54

Bài 2:
c: \(222_{10}=\text{11011110}_2\)
d: \(212_{10}=\text{11010100}_2\)
e: \(3BD_{16}=957_{10}\)
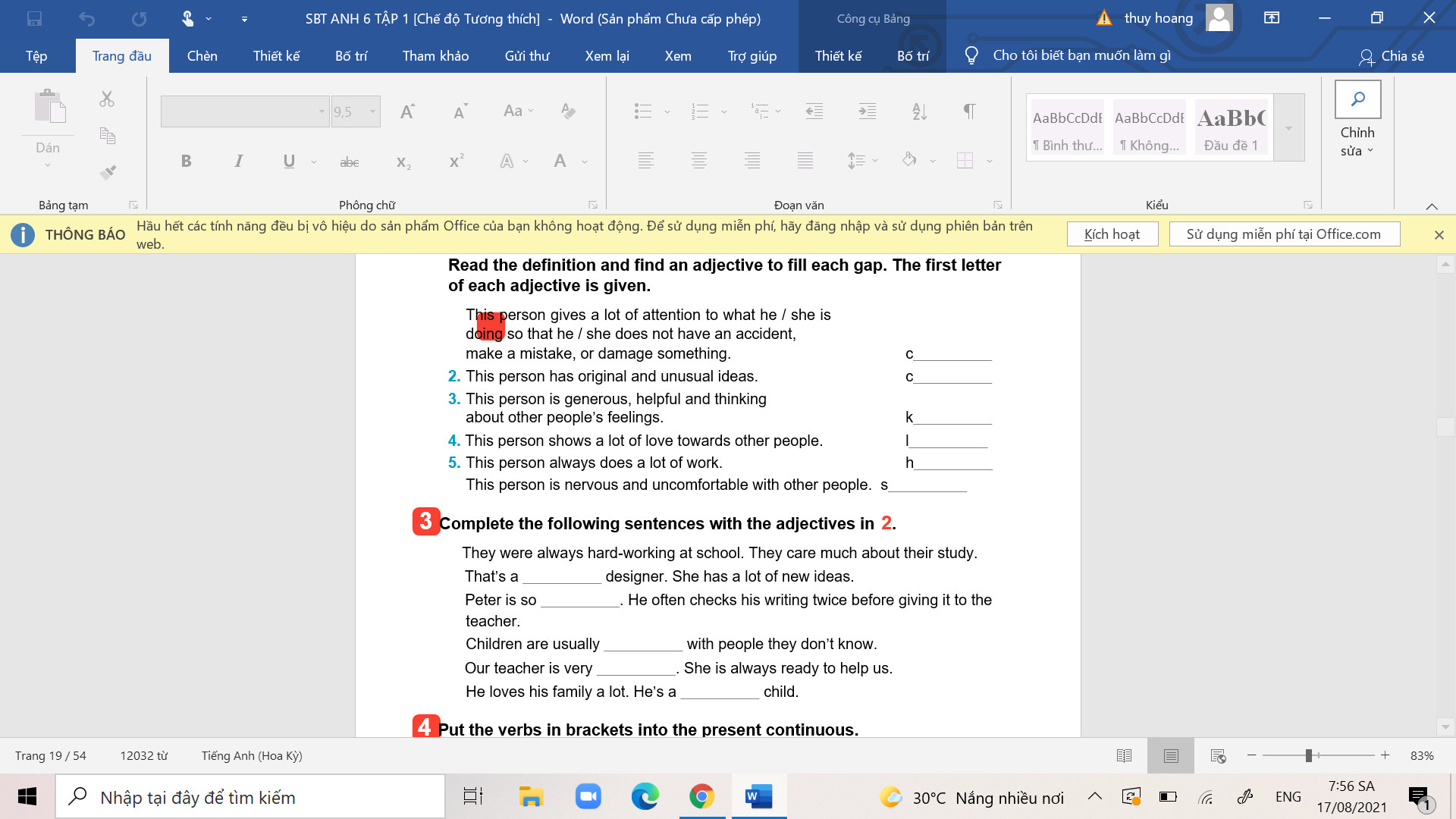 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.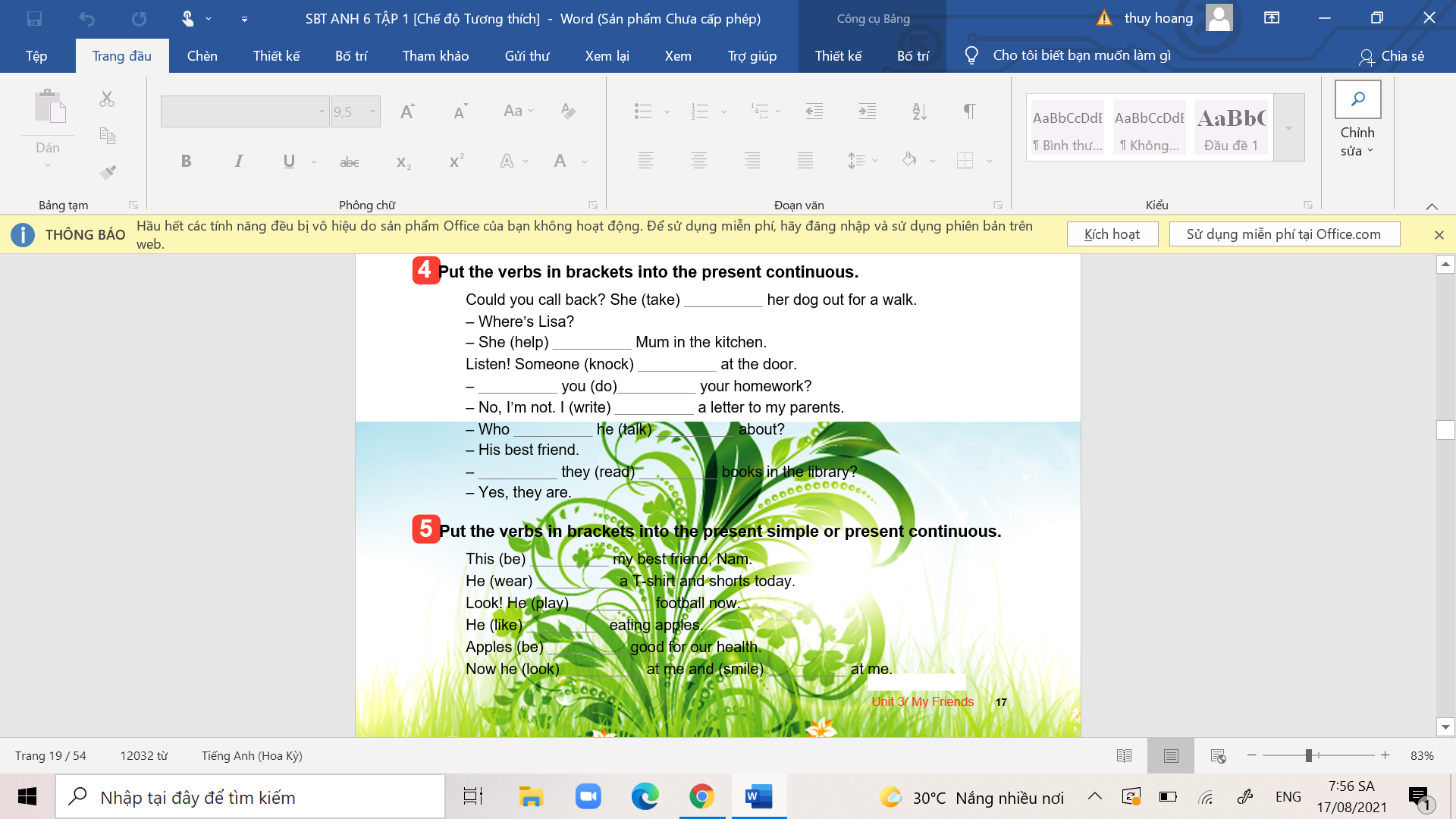 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé. 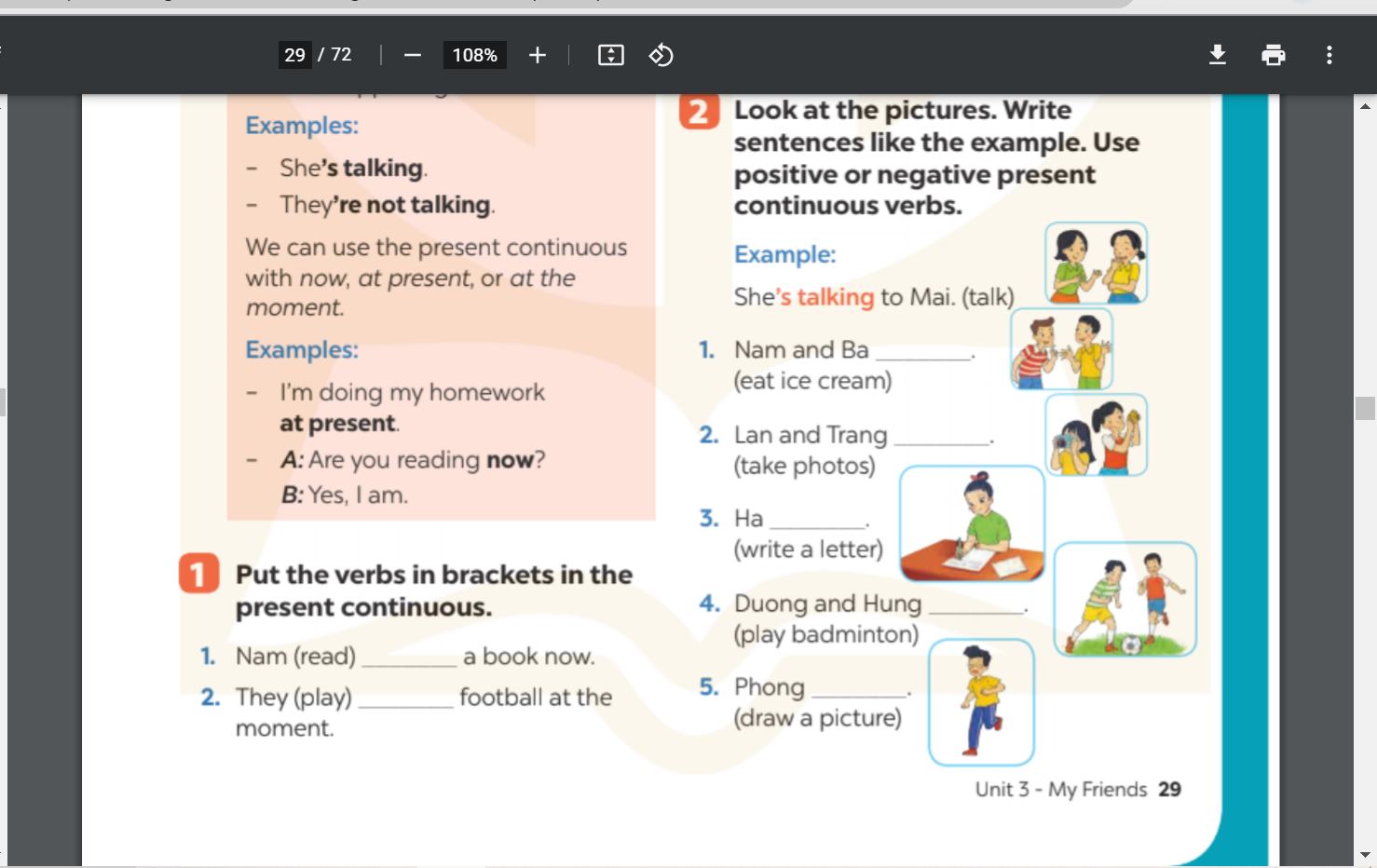
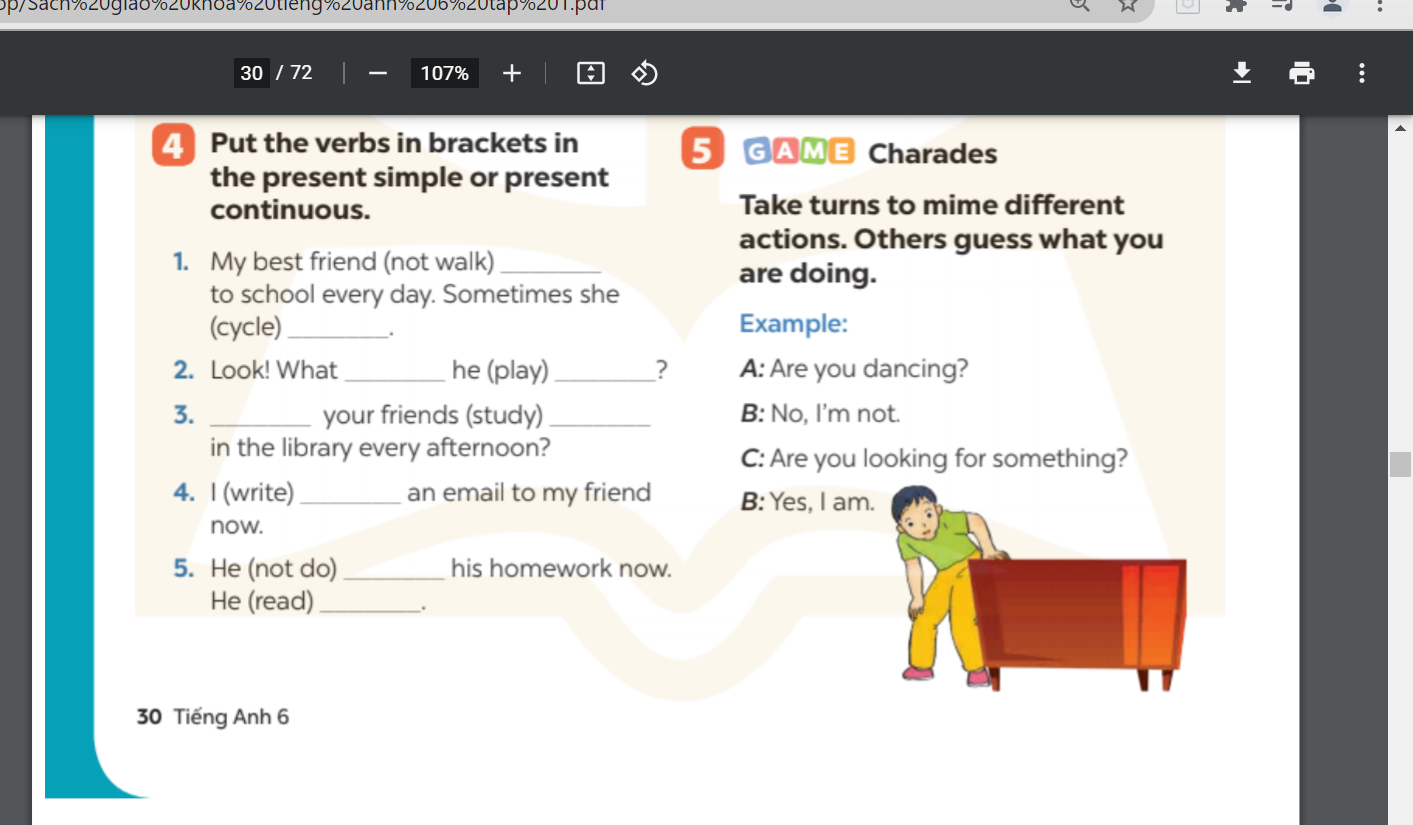 các bn giúp mình bài 4, trang 30 hình ở trên ạ
các bn giúp mình bài 4, trang 30 hình ở trên ạ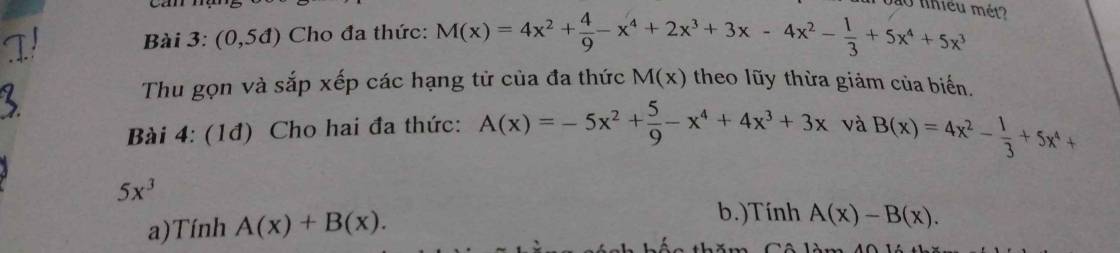
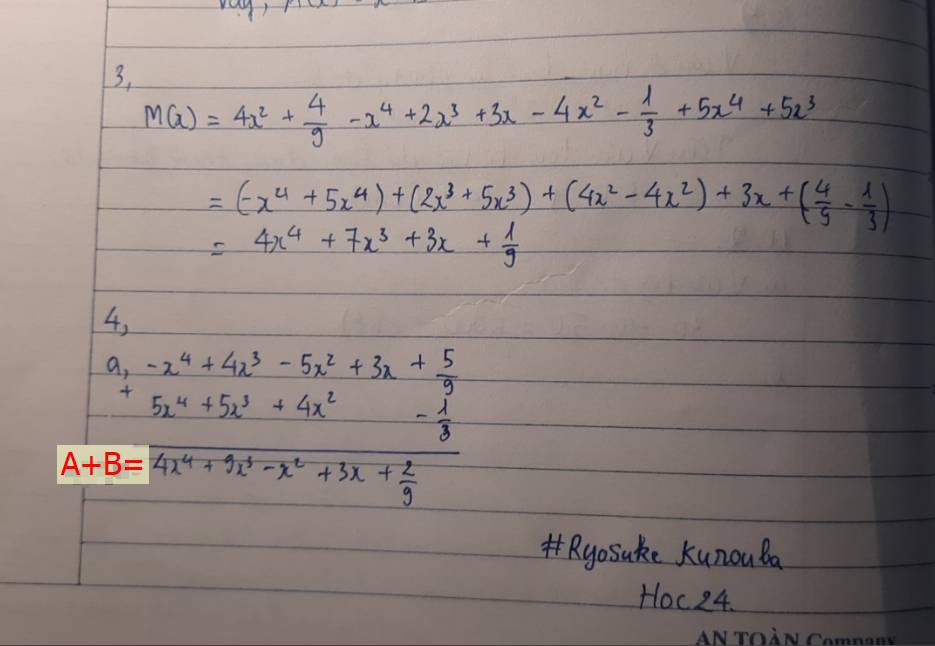
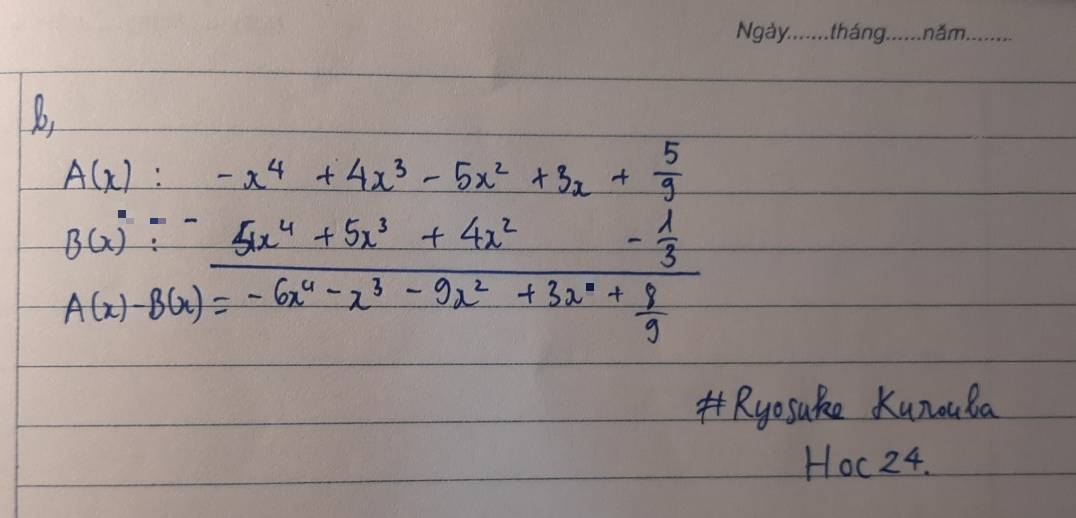
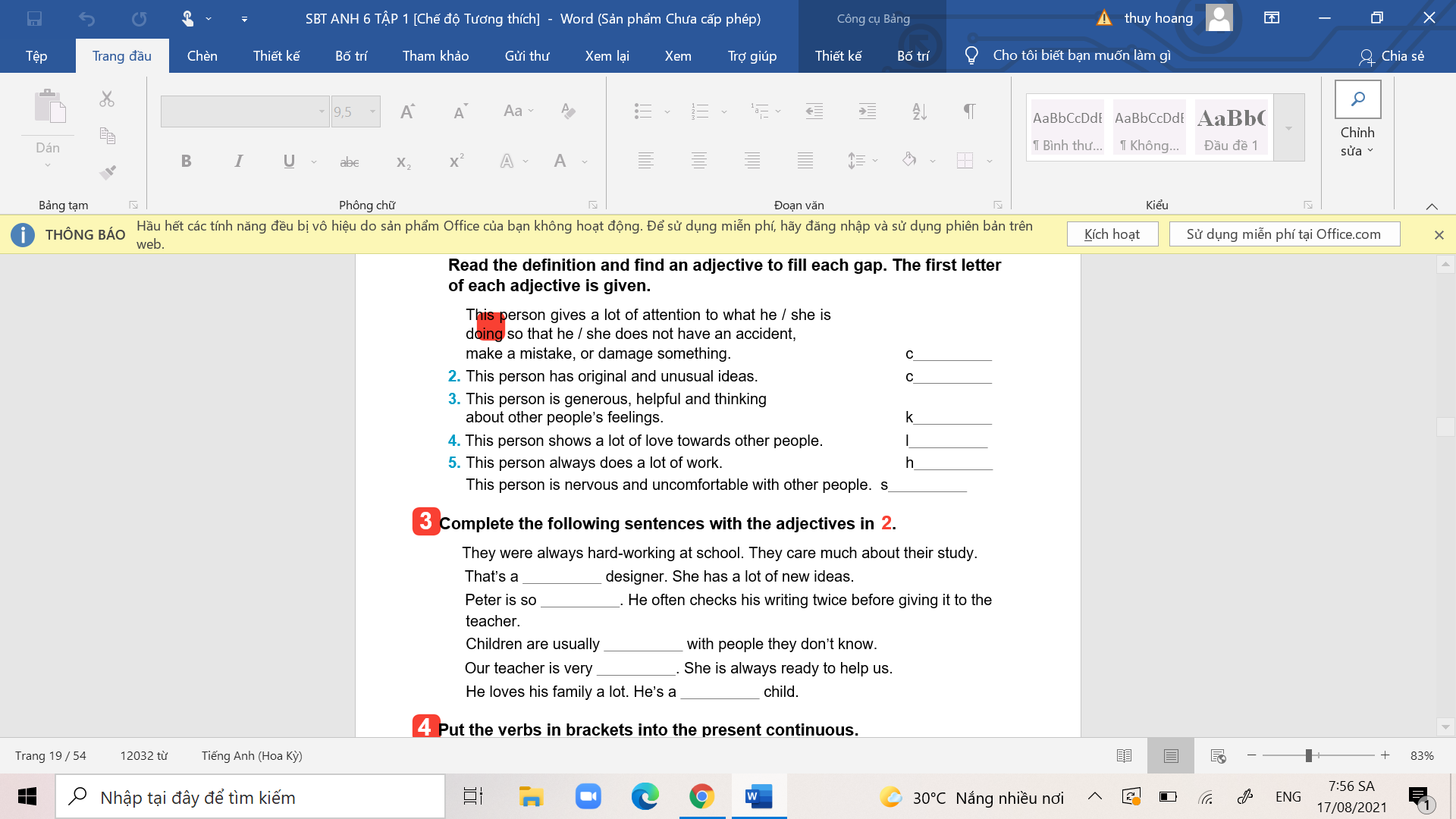 bài 2, bài 3 ạ
bài 2, bài 3 ạ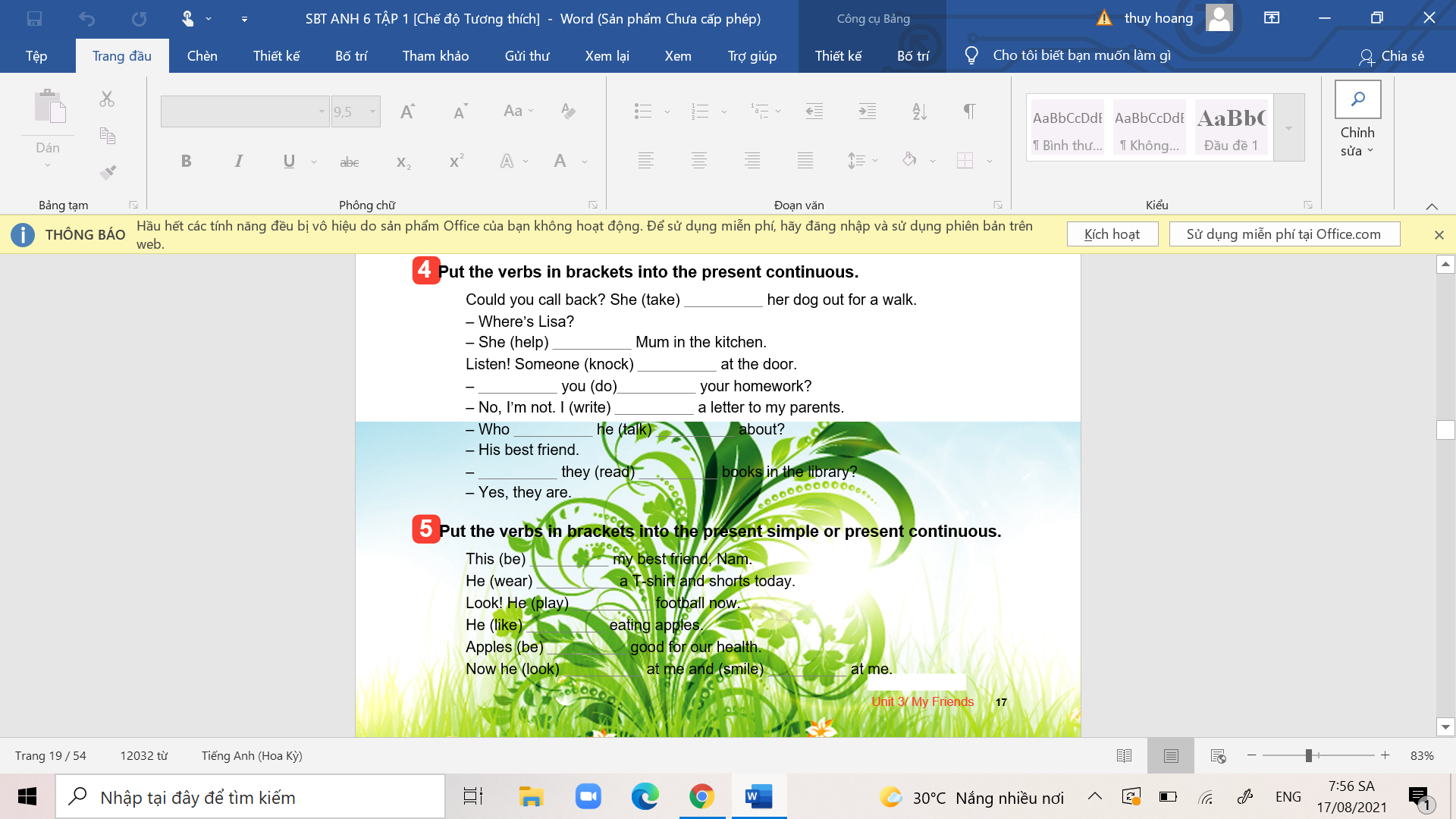


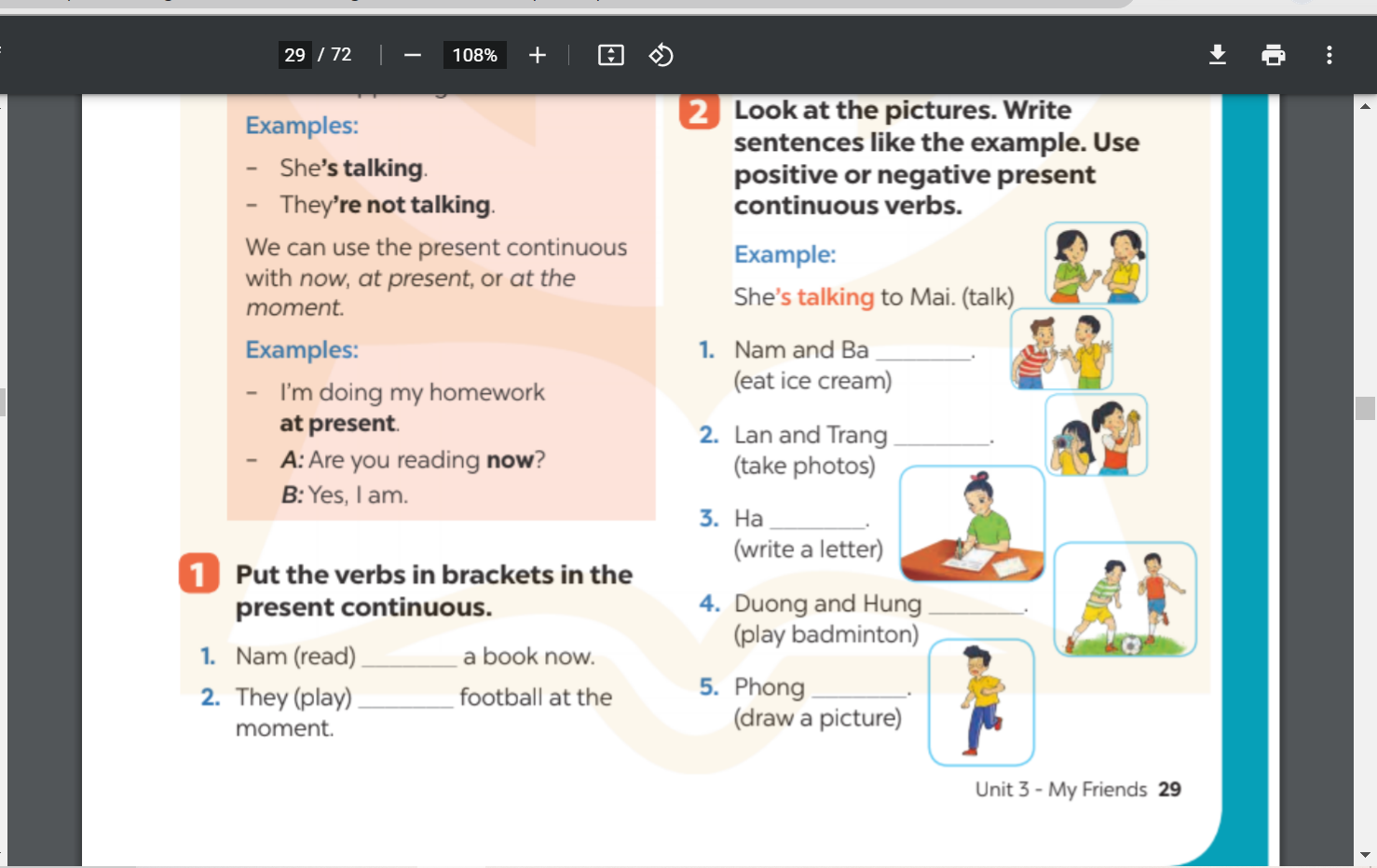 các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ
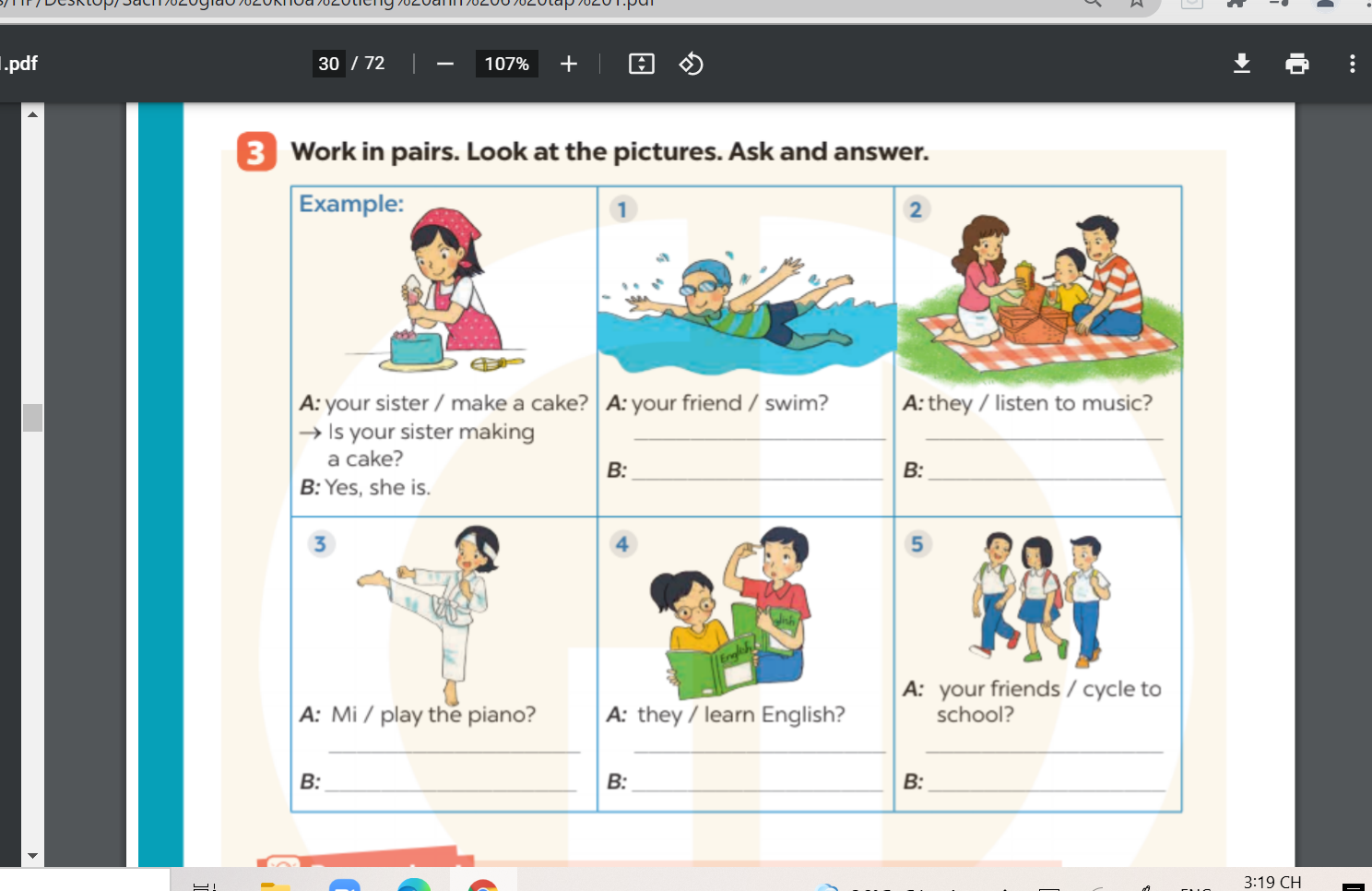
các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ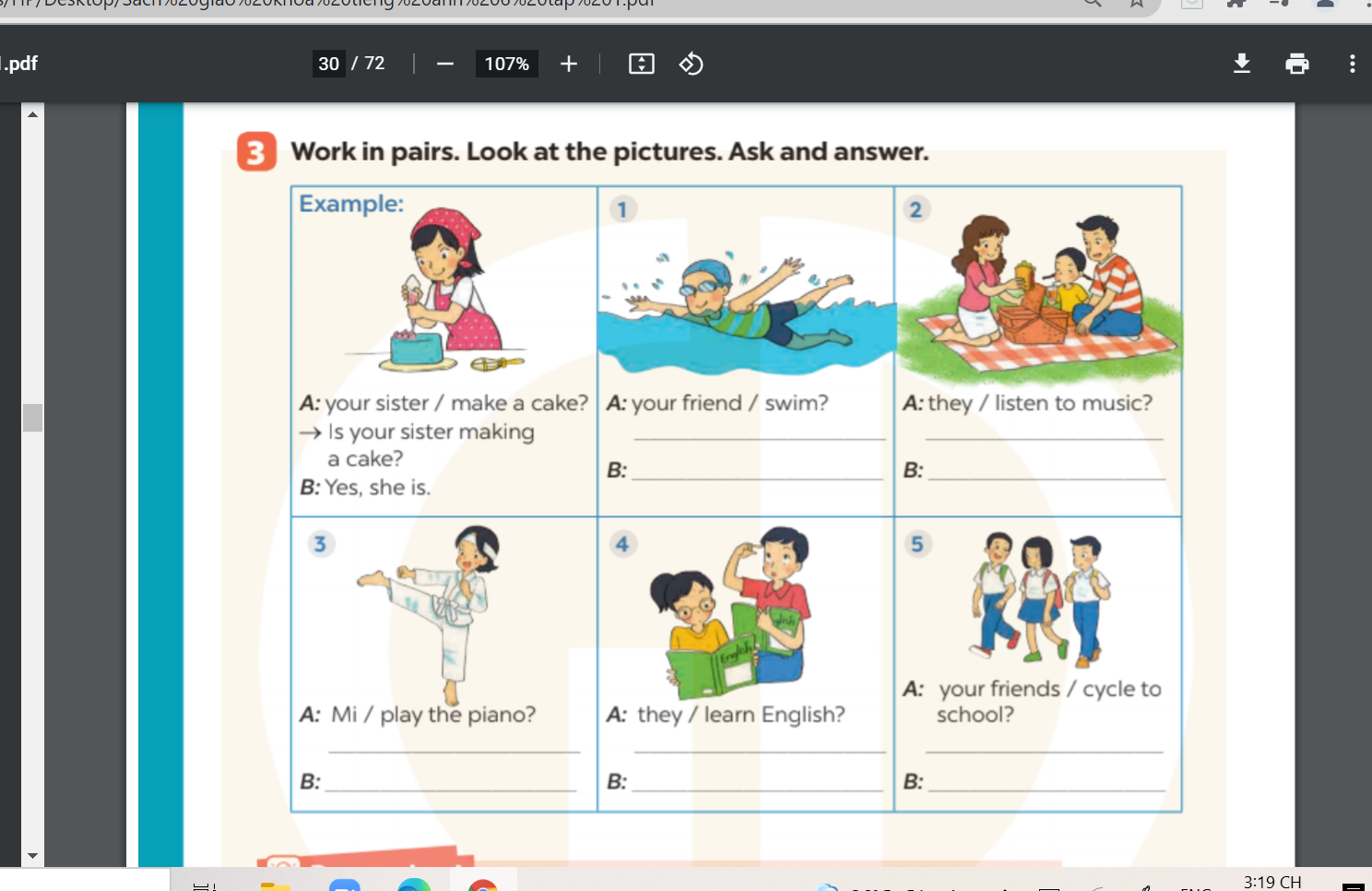 các bạn giúp mình bài 3 hình ở trên đó ạ
các bạn giúp mình bài 3 hình ở trên đó ạ




Do \(\dfrac{SM}{SB}\ne\dfrac{SN}{SA}\Rightarrow MN\) ko song song AB
Trong mp (SAB), kéo dài MN cắt AB tại F
\(\left\{{}\begin{matrix}F\in MN\in\left(AMN\right)\\F\in AB\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow DF=\left(DMN\right)\cap\left(ABCD\right)\)
b.
Do O là tâm đáy \(\Rightarrow\) O là trung điểm AC
Mà G là trọng tâm tam giác ABC \(\Rightarrow\dfrac{OG}{OB}=\dfrac{1}{3}\)
Lại có O là trung điểm BD, M là trung điểm SB
\(\Rightarrow\) E là trọng tâm tam giác SBD \(\Rightarrow\dfrac{OE}{OS}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{OG}{OB}=\dfrac{OE}{OS}\Rightarrow EG||SB\)
\(\Rightarrow EG||\left(SBC\right)\)