Giải hộ mình câu 11 với ah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
!
HP
1 tháng 9 2021
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
HP
1 tháng 9 2021
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
A
1
A
0
DD
0
21 tháng 4 2023
bài 10 : X x 10= 1,643+7,357 410-X= 91,08 : 3,6
X x 10 = 9 410-X=25,3
X = 9 : 10 X=410-25,3
X = 0,9 X = 384,7
T
24 tháng 5 2021
Giải :
-7/12 + 11/8 - 5/9
= 17/72
Học tốt !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
24 tháng 5 2021
lấy tổng của 7/12 và 11/8 trừ đi 5/9 bằng 17/72
#hok tốt
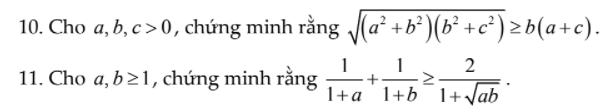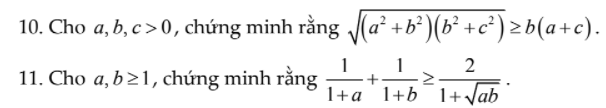
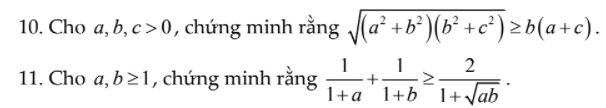
CTHH của oxit là $RO$
$RO + 2HCl \to RCl_2 + H_2O$
$n_{HCl} = 0,2.1 = 0,2(mol)$
Theo PTHH : $n_{RO} = \dfrac{1}{2}n_{HCl} = 0,1(mol)$
$\Rightarrow M_{RO} = R + 16 = \dfrac{4}{0,1} = 40$
$\Rightarrow R = 24(Magie)$