chứng minh định lí : hai tia phân giác của hai góc kề bù vuông góc với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xin lỗi nha tớ ngại đánh máy lắm( mà cũng không biết giải nữa)

Tham khảo nhé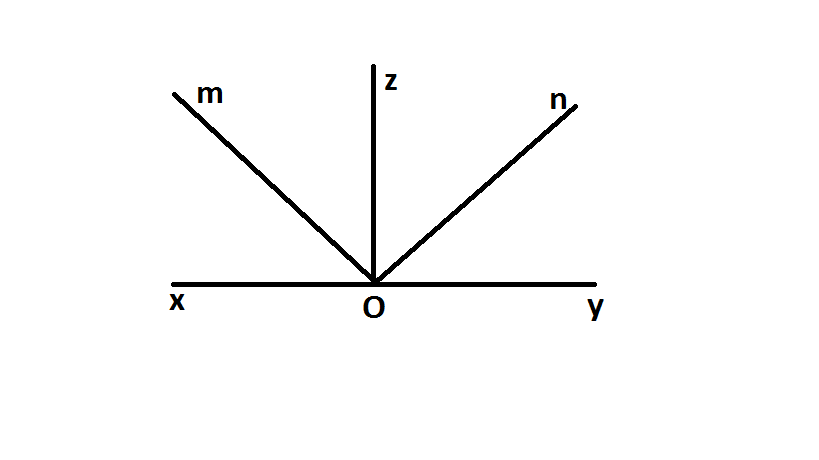
Ta có góc \(\widehat{\text{xOz}}\) + \(\widehat{\text{zOy}}\) = 180\(^o\)(kề bù)
=> 2(\(\widehat{mOz}\) +\(\widehat{zOn}\)) = 180\(^o\)
=> \(\widehat{mOz}\) + \(\widehat{zOn}\) = 90\(^o\)
=>\(\widehat{mOn}\) = 90\(^o\) (vì \(\widehat{xOz}\), \(\widehat{xOz}\) kề nhau)
=> Tia Om vuông góc tia On
Vậy 2 tia phân giác của 1 cặp góc kề bù thì vuông góc với nhau

Giả sử góc xOy bẹt, tia Oz và Om,On lần lượt là phân giác góc xOz và yOz
\(\Rightarrow\widehat{mOn}=\widehat{mOz}+\widehat{zOn}=\dfrac{1}{2}\widehat{xOz}+\dfrac{1}{2}\widehat{yOz}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot180^0=90^0\)
Do đó Om vuông góc On
Suy ra đpcm

O x y z m m 1 2 3 4
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
x y O z t t'
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.

Ta có \(A_1=A_2;A_3=A_4\)
Có \(A_1+A_2+A_3+A_4=180\)
\(\Rightarrow2\left(A_2+A_3\right)=180\)
\(\Rightarrow A_2+A_3=90\)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

Ta có:góc yOn=1/2 góc xOy(On là tia phân giác của góc xOy)
Góc yOn =1/2 góc yOz(On là tia phân giác của góc yOz)
Suy ra: góc yOm+góc yOn=1/2 góc xOy+1/2 góc yOz
Suy ra góc mOn=1/2(góc xOy+góc yOz)
=1/2.180 độ =90 độ
Vậy góc mOn =90 độ


a: 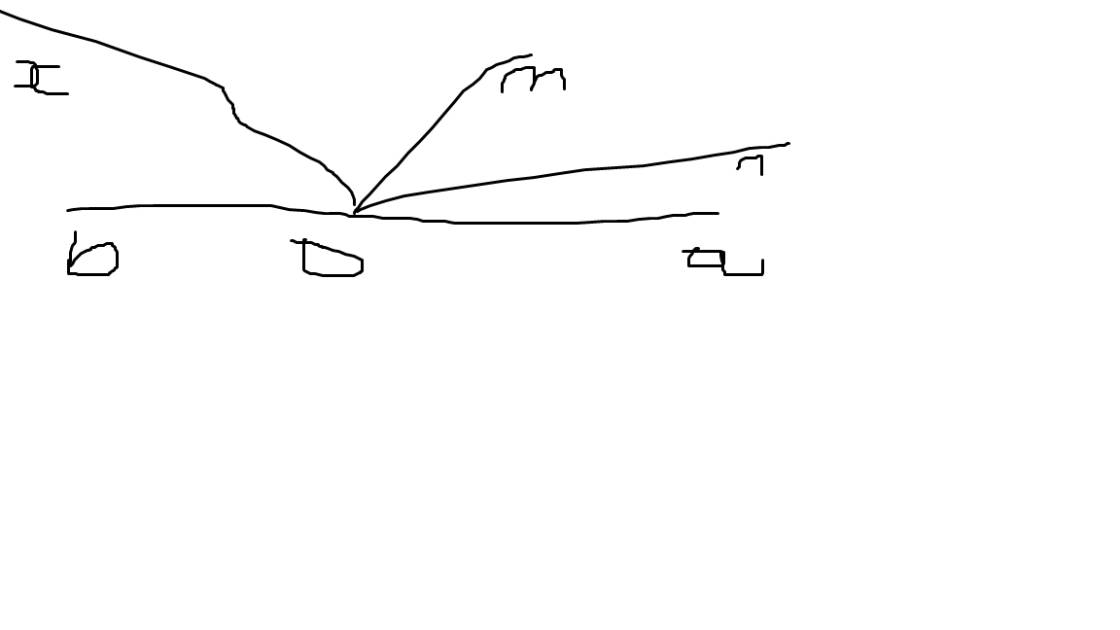
b:
| GT | góc aOm và góc bOm là hai góc kề bù On,Ox lần lượt là phân giác của góc aOm và góc bOm |
| KL | góc xOn=90 độ |
tham khảo :
hình? Gt, kl? Hướng chứng minh? Làm cái gì mà sơ sài v?