Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
c: ΔMAB=ΔMDC
=>\(\widehat{MBA}=\widehat{MCD}\)
Xét ΔABH vuông tại H và ΔDCK vuông tại K có
AB=DC
\(\widehat{ABH}=\widehat{DCK}\)
Do đó: ΔABH=ΔDCK
=>BH=CK
BH+HK=BK
CK+HK=CH
mà BH=CK
nen BK=CH
d: Xét tứ giác ABCE có
I là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//CE và AB=CE
Ta có: AB//CE
AB//CD
CD,CE có điểm chung là C
Do đó: C,E,D thẳng hàng
Ta có: AB=EC
AB=CD
Do đó: EC=CD
mà C,E,D thẳng hàng
nên C là trung điểm của DE
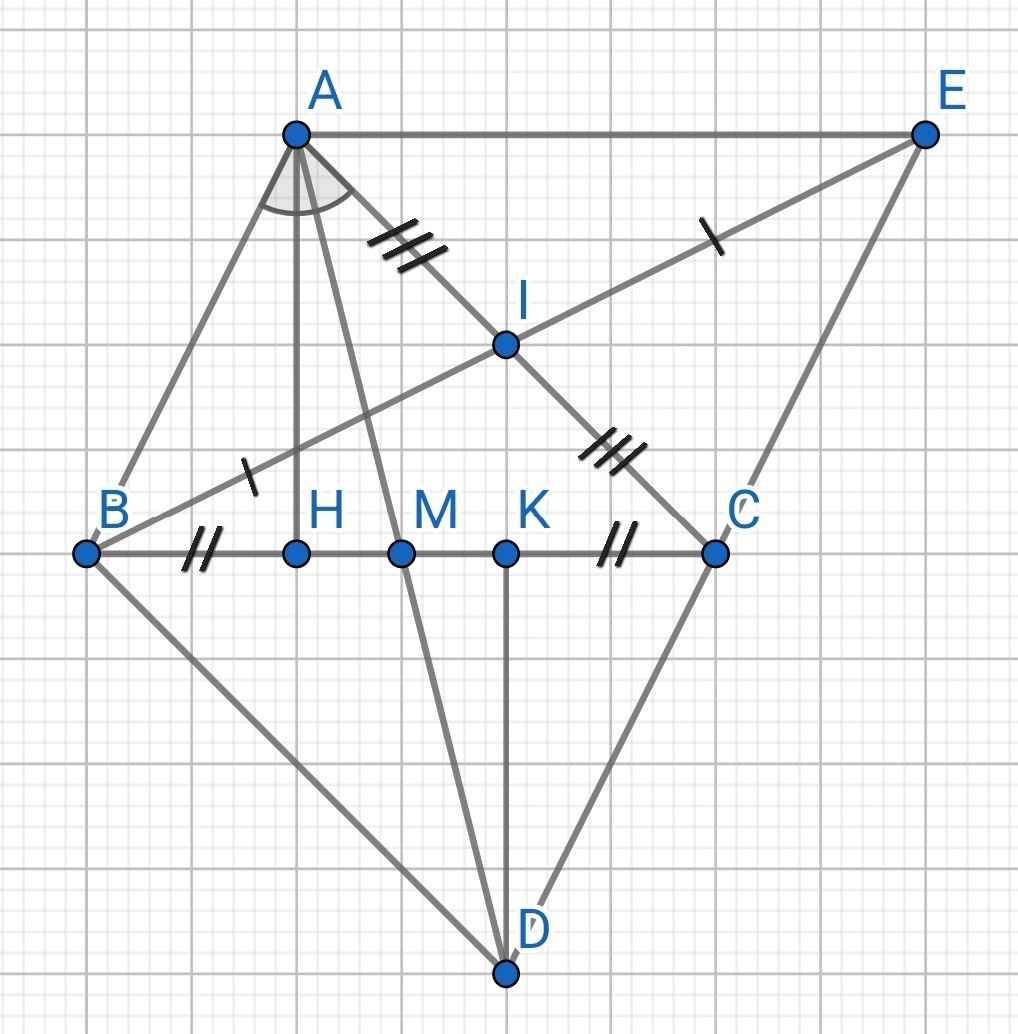c) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét hai tam giác vuông: ∆AHM và ∆DKM có:
MA = MD (gt)
∠AMH = ∠DMK (đối đỉnh)
⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)
⇒ HM = KM (hai cạnh tương ứng)
Ta có:
BK = BM + KM
CH = CM + HM
Mà BM = CM (cmt)
KM = HM (cmt)
⇒ BK = CH
d) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
⇒ AB // DC và AB = DC
Tứ giác ABCE có:
I là trung điểm của AC (gt)
I là trung điểm của BE (gt)
⇒ ABCE là hình bình hành
⇒ AB // CE và AB = CE
Do AB // CE (cmt)
AB // DC (cmt)
⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)
Ta có:
AB = CE (cmt)
AB = DC (cmt)
⇒ CD = CE
⇒ C là trung điểm của DE
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét ΔMBD và ΔMCA có
MB=MC
\(\widehat{BMD}=\widehat{CMA}\)
MD=MA
Do đó: ΔMBD=ΔMCA
=>\(\widehat{MBD}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//AC
c: Xét ΔDKB vuông tại K và ΔAHC vuông tại H có
DB=AC
\(\widehat{DBK}=\widehat{ACH}\)
Do đó: ΔDKB=ΔAHC
=>BK=CH
d: Xét tứ giác ABCE có
I là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//CE và AB=CE
Ta có; ΔMAB=ΔMDC
=>AB=DC
Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
Ta có: AB//DC
AB//CE
DC,CE có điểm chung là C
Do đó: D,C,E thẳng hàng
ta có: AB=CD
AB=CE
Do đó: DC=CE
mà D,C,E thẳng hàng
nên C là trung điểm của DE
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
Bài 11:
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AC//BD
\(a,\left\{{}\begin{matrix}AM=MD\\BM=MC\\\widehat{AMB}=\widehat{CMD}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABM}=\widehat{DCM}\\ \text{Mà 2 góc này ở vị trí so le trong nên }AB\text{//}CD\\ b,AH\bot BC;DK\bot BC\Rightarrow AH\text{//}DK\\ \left\{{}\begin{matrix}AM=MD\\\widehat{AHM}=\widehat{DKM}=90^0\\\widehat{AMH}=\widehat{KMD}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AHM=\Delta DKM\left(c.g.c\right)\\ \Rightarrow AH=DK\)
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
Xét ΔAHM vuông tại H và ΔDKM vuông tại K có
MA=MD
góc AMH=góc DMK
Do đó: ΔAHM=ΔDKM
=>AH=DK