Giúp mình bài 7 với ạ :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2021
Bài 7 :
Pt : ZnO + 2HCl → ZnCl2 + H2O\(|\)
1 2 1 1
a 2a
Fe2O3 + 6HCl → 2FeCl3 + 3H2O\(\)\(|\)
1 6 2 3
b 6b
Gọi a là số mol của ZnO
b là số mol của Fe2O3
Theo đề ta có : mZnO + mFe2O3 = 28,15 (g)
⇒ nZnO . MZnO + nFe2O3 . MFe2O3 = 28,15 g
⇒ 81a + 160b = 28,15 g (1)
Khối lượng của axit clohidric
C0/0HCl = \(\dfrac{m_{ct}.100}{m_{dd}}\Rightarrow m_{ct}=\dfrac{C.m_{dd}}{100}=\dfrac{6.547,5}{100}=32,85\left(g\right)\)
Số mol của axit clohidric
nHCl = \(\dfrac{m_{HCl}}{M_{HCl}}=\dfrac{32,85}{36,5}=0,9\left(mol\right)\)
⇒ 2a + 6b = 0,9 (2)
Từ (1),(2) , ta có hệ phương trình :
81a + 160b = 28,15
2a + 6b = 0,9
⇒ \(\left\{{}\begin{matrix}a=0,15\\b=0,1\end{matrix}\right.\)
Khối lượng của kẽm oxit
mZnO = nZnO . MZnO
= 0,15 . 81
= 12,15 (g)
Khối lượng của sắt (III) oxit
mFe2O3 = nFe2O3 . MFe2O3
= 0,1 . 160
= 16 (g)
0/0ZnO = \(\dfrac{m_{ZnO}.100}{m_{hh}}=\dfrac{12,15.100}{28,15}=43,16\)0/0
0/0Fe2O3 = \(\dfrac{m_{Fe2O3}.100}{m_{hh}}=\dfrac{16.100}{28,15}=56,84\)0/0
Chúc bạn học tốt
10 tháng 10 2021
Bài 6:
a: \(\sqrt{\dfrac{2}{3-\sqrt{5}}}=\dfrac{\sqrt[4]{2}\cdot\left(\sqrt[2]{5}+1\right)}{2}\)
b: \(\sqrt{\dfrac{a-4}{2\left(\sqrt{a}-2\right)}}=\dfrac{\sqrt{2}\left(\sqrt{a}+2\right)}{2}\)
TP
12 tháng 7 2021
7. a) Hợp chất X của A với C: ACx
Ta có: \(\dfrac{A}{A+12x}.100=62,5\)
Lập bảng:
| x | 1 | 2 | 3 |
| A | 20 | 40 | 60 |
| Kết luận | Loại | Chọn (Ca) | Loại |
Vậy nguyên tố A là Ca
CTPT của hợp chất X : CaC2
CTCT:
b)Gọi số oxh của C trong chất là x. Ta có số oxh của Ca là +2
Trong CaC2: 2 + 2. x = 0 → x = -1
Số oxh của C trong CaC2 là -1
giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Lời giải:
a. Để $n$ là phân số thì $n-6\neq 0$ hay $n\neq 6$
b. Để $A$ nguyên thì $n+9\vdots n-6$
$\Rightarrow (n-6)+15\vdots n-6$
$\Rightarrow 15\vdots n-6$
$\Rightarrow n-6\in\left\{\pm 1; \pm 3; \pm 5; \pm 15\right\}$
$\Rightarrow n\in\left\{7; 5; 9; 3; 11; 1; -9; 21\right\}$
Do $n$ là số tự nhiên lớn hơn $0$ nên $n\in\left\{7; 5; 9; 3; 11; 1; 21\right\}$
c.
Để $A$ tự nhiên thì $A>0$ và $A$ nguyên
$A>0$ khi mà $n-6>0$ hay $n>6$
$A$ nguyên khi mà $n\in\left\{7; 5; 9; 3; 11; 1; 21\right\}$ (đã cm ở phần b)
Suy ra để $A>0$ và nguyên thì $n\in\left\{7; 9; 11; 21\right\}$
AH
Akai Haruma
Giáo viên
21 tháng 11 2023
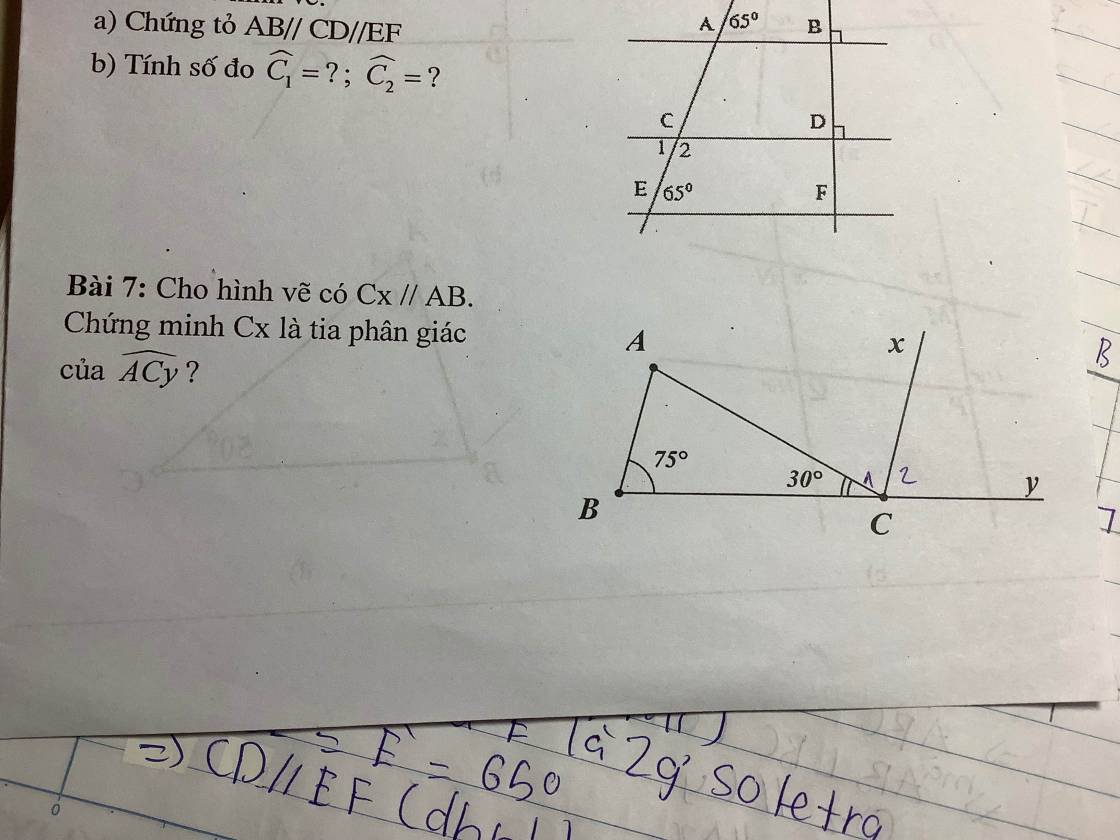
Bài 7:
Vì $Cx\parallel AB$ nên:
$\widehat{C_1}=\widehat{BAC}$ (2 góc so le trong)
$=180^0-\widehat{ABC}-\widehat{ACB}=180^0-75^0-30^0=75^0$
$\widehat{C_2}=180^0-\widehat{ACB}-\widehat{C_1}$
$=180^0-30^0-75^0=75^0$
$\Rightarrow \widehat{C_1}=\widehat{C_2}$
$\Rightarrow Cx$ là tia phân giác của $\widehat{ACy}$
AH
Akai Haruma
Giáo viên
21 tháng 11 2023
Bài 6:
a. Ta thấy $AB\perp BD, CD\perp BD\Rightarrow AB\parallel CD(1)$
$CD\perp DF, EF\perp DF\Rightarrow CD\parallel EF(2)$
Từ $(1); (2)\Rightarrow AB\parallel CD\parallel EF$
b.
Vì $CD\parallel EF$ nên:
$\widehat{C_1}=\widehat{CEF}=65^0$ (2 góc so le trong)
$\widehat{C_2}=180^0-\widehat{C_1}=180^0-65^0=115^0$
Bài 7:
a) Xét ΔACH vuông tại H và ΔBCA vuông tại A có
\(\widehat{ACH}\) chung
Do đó: ΔACH\(\sim\)ΔBCA(g-g)
Bài 7:
b) Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH\(\sim\)ΔCBA(g-g)
Suy ra: \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)