cho hình chữ nhật ABCD có DT 240 cm2. M là điểm trên của AB sao cho AM bằng 1/3 AB. nối D với M. tính diện tích tam giác AMD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
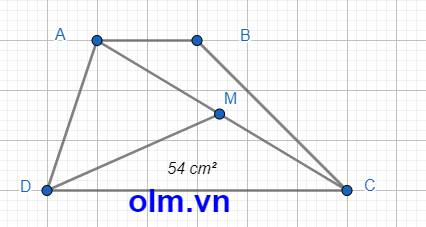
SMDC = \(\dfrac{1}{2}\)SACD (Vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AC và MC = \(\dfrac{1}{2}\)AC)
⇒SACD = SMDC \(\times\) 2 = 54 \(\times\) 2 = 108 (cm2)
SABC = \(\dfrac{1}{3}\)SADC ( vì hai tam giác có chiều cao bằng chiều cao của hình thang và AB = \(\dfrac{1}{3}\)CD)
⇒SABC = 108 \(\times\) \(\dfrac{1}{3}\) = 36 (cm2)
SABCD = SABC + SACD = 36 + 108 = 144 (cm2)
26 tháng 3 2016
lấy m nằm bất kì trên đoạn ab => samd + smbc = smcd=sabcd/ 2
tổng diện tích tam giác amd + mbc = 96/42 = 48 ( cm 2)
26 tháng 3 2016
Đề bài :
Cho hình chữ nhật ABCD có diện tích bằng 425,6 cm2 . Trên AB lấy điểm M . Tính tổng diện tích tam giác AMD và MBC .
Bài giải :
Ta có hình vẽ sau :
Vậy hình chữ nhật ABCD được chia ra làm ba hình . Ta thấy hình MCD bằng hai hình AMD và MBC .
Suy ra tổng diện tích tam giác AMD và BMC là :
425,6 : 2 = 212,8 ( cm2 )
Đáp số : 212,8 cm2 .
6 tháng 4 2016
ta có hình vẽ:
diện tích hình MCD=1/2 ABCD nên diện tích MCD là:
200:2=100(cm2)
vì N là trung điểm là 1/2 chiều cao cho nên diện tích NCD lá:
100:2=50(cm2)
Tam giác AMD có đáy AM = 1/3 AB và đường cao tương ứng chính là chiều rộng hình chữ nhật
S(AMD) = AM x AD : 2 = 1/6AB x AD
Mà S(ABCD) = AB x AD
Nên S(AMD) = 1/6 S(ABCD)
DT tam giác AMD :
240 : 6 = 40 cm2