Trong mặt phẳng Oxy, cho đường thẳng d:5x-2y+3=0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép quay tâm O, góc quay -180 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) d 1 : 3x + 2y + 6 = 0
b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0

Qua phép đối xứng tâm O biến điểm M(x; y) thuộc đường thẳng d thẳng điểm M’ (x’; y’) thuộc đường thẳng d’.
Ta có: x ' = − x y ' = − y ⇔ x = − x ' y = − y '
Vì điểm M thuộc d nên: 3x – 2y – 1 = 0
Suy ra: 3. (-x’) – 2(- y’) -1 = 0 hay - 3x’ + 2y’ – 1=0
Vây phương trình đường thẳng d’ là - 3x + 2y - 1= 0
Đáp án B

Dễ thấy d và d' không song song với nhau.
Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'.
Từ đó suy ra Δ có phương trình:
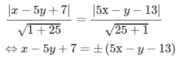
Từ đó tìm được hai phép đối xứng qua các trục:
Δ 1 có phương trình: x + y – 5 = 0,
Δ 2 có phương trình: x – y – 1 = 0.

Lấy M(2; 1) thuộc d, phép quay Q ( O ; 90 o ) biến M(2; 1) thành M’(-1; 2). Tâm quay O(0; 0) thuộc d ⇒ d' đi qua O và M’ có phương trình 2x + y = 0.
Đáp án B

Giao của d và d' với lần lượt là A(−2; 0) và A′(8;0). Phép đối xứng qua tâm cần tìm biến A thành A' nên tâm đối xứng của nó là I = (3;0).

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

Chọn đáp án D.
Đường thẳng song song với d có phương trình -2x + 4y -1 = 0
Lấy A(3;9) thuộc (d)
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_{A'}+3=0\\y_{A'}+9=0\end{matrix}\right.\Leftrightarrow A'\left(-3;-9\right)\)
Vì (d1)//(d) nên (d1): 5x-2y+c=0
Thay x=-3 và y=-9 vào (d1), tađược:
c+5*(-3)-2*(-9)=0
=>c-15+18=0
=>c=-3