Mn giúp em với ạ,em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
mn giúp em và giair thích giúp em với ạ em cảm ơn mn
1
28 tháng 1 2023
2. get lucky money
3. talent show
4. always
5. food stands
6. fireworks
7. never
8. eat traditional foods
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
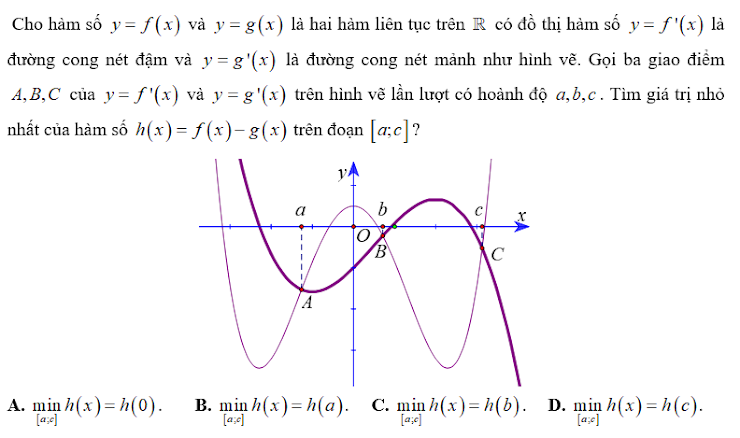
\(h'\left(x\right)=f'\left(x\right)-g'\left(x\right)=0\Rightarrow x=\left\{a;b;c\right\}\)
Ta thấy \(h'\left(x\right)>0\) trên \(\left(b;c\right)\) và \(h'\left(x\right)< 0\) trên \(\left(a;b\right)\)
\(\Rightarrow x=b\) là điểm cực tiểu trên \(\left[a;c\right]\) hay \(\min\limits_{\left[a;c\right]}h\left(x\right)=h\left(b\right)\)
NQ
0
TT
0
LC
1
3 tháng 8 2021
\(=>Qthu1=0,2.340000=68000J\)
\(=>Qthu2=2100.0,2.20=8400J\)
\(=>Qtoa=2.4200.25=210000J\)
\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn
\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)
\(=>tcb=14,5^oC\)
3 tháng 8 2021
Cho em hỏi ngu tí ạ vậy tcb ở nhưng phép tính trên vứt đi đâu ạ
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2021
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{3x-1}=a\\\sqrt[3]{x+1}=b\\\sqrt[3]{-2x}=c\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+b=c\\a^3+b^3=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\\left(a+b\right)^3-3ab\left(a+b\right)=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c^3-3abc=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left(c^2-ab\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+b\right)^2-ab\right]=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\right]=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=0\\a=b=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt[3]{-2x}=0\Leftrightarrow x=0\)
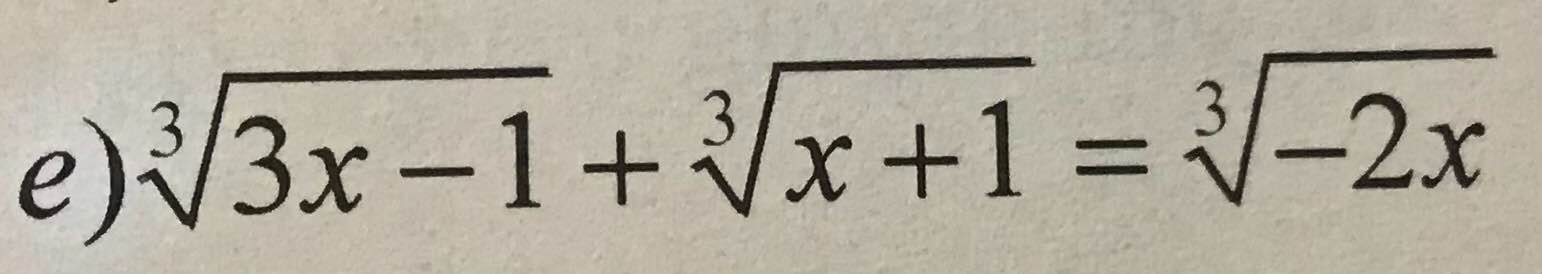
a: Xét tứ giác MAOC có góc MAO+góc MCO=180 độ
nên MAOC là tứ giác nội tiếp
b: ΔOBC cân tại O
mà OK là trung tuyến
nên OK là đường phân giác và OK vuông góc với BC
Xét ΔOBN và ΔOCN có
OB=OC
góc BON=góc CON
ON chung
Do đó: ΔOBN=ΔOCN
=>NB=NC
=>NB^2=NC^2=NK*NO