Cho △ABC đồng dạng với △MNP. Biết AB= 3cm, MN=2cm, diện tích của △ABC bằng 36cm2 .
a) Tính tỉ số đồng dạng k của hai tam giác.
b) Tính diện tích của tam giác MNP.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
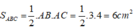
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
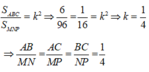
Thay số
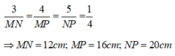
Chọn đáp án B

Ta có : Vì tam giác DEF đồng dạng với tam giác MNP theo tỉ số k=\(\dfrac{1}{2}\)
=> \(\dfrac{S_{DEF}}{S_{MNP}}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
=> \(S_{MNP}=\dfrac{S_{DEF}}{\dfrac{1}{4}}=\dfrac{6}{\dfrac{1}{4}}=24\left(cm^2\right)\)
Ta có: ΔDEF\(\sim\)ΔMNP theo tỉ số \(k=\dfrac{1}{2}\)(gt)
nên \(\dfrac{S_{DEF}}{S_{MNP}}=k^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{6}{S_{MNP}}=\dfrac{1}{4}\)
hay \(S_{MNP}=24\left(cm^2\right)\)

Giả sử ΔMNP ~ ΔQRS theo tỉ số diện tích S M N P S Q R S = k 2
Đáp án: C

Lời giải:
Nếu 2 tam giác đồng dạng với tỉ số $k$ thì tỉ số diện tích của chúng là $k^2$.
Ứng vào bài toán:
\(\frac{S_{ABC}}{S_{MNP}}=0,25^2=\frac{1}{16}\)
Ta có: ΔABC\(\sim\)ΔMNP theo tỉ số đồng dạng k=0,25
\(\Leftrightarrow\dfrac{S_{ABC}}{S_{MNP}}=k^2=\left(0.25\right)^2=0.0625\)

a) Xét\(\Delta AMN\)và \(\Delta ABC\)có:
\(\widehat{A}\)chung
\(\frac{AM}{MB}=\frac{AN}{NC}\)
\(\Rightarrow\Delta AMN\)đồng dạng \(\Delta ABC\)
Tỉ số đồng dạng \(\frac{1}{2}\)
bn ơi, sao bn bt tỉ số đồng dạng là 1/2 vậy? mình không hiểu chỗ này lắm
a, △ABC~△MNP => AB/MN=3/2 => k=3/2
b, SABC/SMNP=k2=9/4
=> 36/SMNP=9/4 => SMNP=16 cm2