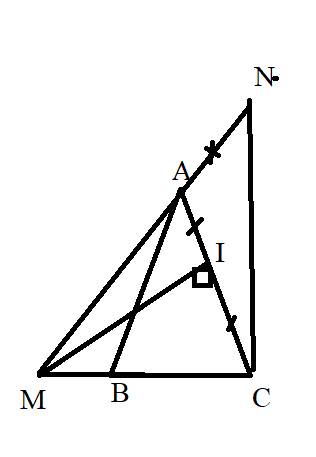
Cho tam giác ABC từ A dựng đường thẳng d1 vuông góc với AB từ A dựng đường thẳng d2 vuông góc với AC. Trên d1 lấy M, trên d2 lấy N sao cho AM=AN. CMR
a) Tam giác ABM = Tam giác ACN
b) Gọi giao của MB Và NC là O, OI là teung điểm của BC. CM A,O,I thẳng hàng
c) CM : MN // BC