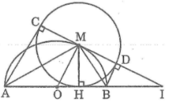
cho nửa đường tròn tâm O đường kính AB.Lấy điểm C thuộc nửa đường tròn sao cho AC<CB.Qua điểm B vẽ tiếp tuyến Bx với nửa đường tròn.Qua điểm O vẽ đườn thẳng vuông góc với BC tại H và cắt tiếp tuyến Bx tại D
a,CMR:\(BD^2\) =DH.DO
b,Đường thẳng AD cắt nửa đường tròn tại E.CM AEB vuông tại E và HD.DO=DE.DA
c,Chứng minh DC là tiếp tuyến của đường tròn và góc DEC = góc DCA

a/
Xét tg vuông BHD và tg vuông OBD có
\(\widehat{ODB}\) chung
=> tg BHD đồng dạng với tg OBD
\(\Rightarrow\dfrac{BD}{DO}=\dfrac{DH}{BD}\Rightarrow BD^2=DH.DO\) (đpcm)
b/
Xét tg AEB có
\(\widehat{AEB}=90^o\) (góc nội tiếp chắn nửa đường tròn) (đpcm)
Ta có \(BD^2=HD.DO\) (cmt) (1)
Xét tg vuông BED và tg vuông ABD có
\(\widehat{ADB}\) chung
=> tg BED đồng dạng với tg ABD
\(\Rightarrow\dfrac{BD}{DA}=\dfrac{DE}{BD}\Rightarrow BD^2=DE.DA\) (2)
Từ (1) và (2) => HD.DO = DE.DA (đpcm)
c/
Xét tg DBC có
DB=DC (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn)
=> tg DBC cân tại D
Ta có \(DH\perp BC\)
=> \(\widehat{ODC}=\widehat{ODB}\) (trong tg cân đường cao xuất phát từ đỉnh đồng thời là đường phân giác)
Xét tg OCD và tg OBD có
DC=DB (cmt)
OD chung
\(\widehat{ODC}=\widehat{ODB}\) (cmt)
=> tg OCD = tg OBD (c.g.c)
\(\Rightarrow\widehat{OCD}=\widehat{OBD}=90^o\) => DC là tiếp tuyến của (O) (đpcm)
ta có
\(sđ\widehat{DCE}=\dfrac{1}{2}sđ\) cung CE (góc nt đường tròn)
\(sđ\widehat{CAD}=\dfrac{1}{2}sđ\) cung CE (góc nt đường tròn)
\(\Rightarrow\widehat{DCE}=\widehat{CAD}\) (1)
Xét tg ECD có \(\widehat{DEC}=180^o-\widehat{DCE}-\widehat{ADC}\) (2)
Xét tg DAC có \(\widehat{DCA}=180^o-\widehat{CAD}-\widehat{ADC}\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{DEC}=\widehat{DCA}\) (đpcm)