biểu thức rút gọn của sin4x*cos2x-sin3x*cosx là biểu thức nào
giúp vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LS
1
Những câu hỏi liên quan
DM
2
2
6 tháng 5 2022
`A=[sin x + sin 2x + sin 3x]/[cos x + cos 2x + cos 3x]`
`A=[2sin2x.cosx+sin2x]/[2cos2x.cosx+cos2x]`
`A=[sin2x(2cosx+1)]/[cos2x(2cosx+1)]`
`A=tan 2x`
6 tháng 5 2022
\(A=\dfrac{sinx-sin2x+sin3x}{cosx-cos2x+cos3x}\)
\(ĐK\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(A=\dfrac{sinx+sin3x-sin2x}{cosx+cos3x-cos2x}\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}=\dfrac{2sin2x.cosx-sin2x}{2cos2x.cosx-cos2x}\\=\dfrac{sin2x\left(2cosx-1\right)}{cos2x\left(2cosx-1\right)}\end{matrix}\right.\) \(\Rightarrow\) \(A=tan2x\)
M
14 tháng 6 2020
\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)
CM
8 tháng 1 2019
Đáp án: A
Ta có:
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 6 2020
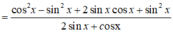
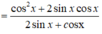
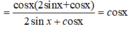
\(cos^2x-\left(2sin\frac{x}{2}cos\frac{x}{2}\right)^2=cos^2x-sin^2x=cos2x\)
\(\frac{sin3x}{sinx}-\frac{cos3x}{cosx}=\frac{sin3x.cosx-cos3x.sinx}{sinx.cosx}=\frac{sin\left(3x-x\right)}{\frac{1}{2}sin2x}=\frac{2sin2x}{sin2x}=2\)
\(\frac{cosx+cos3x+cos2x+cos4x}{sinx+sin3x+sin2x+sin4x}=\frac{2cosx.cos2x+2cosx.cos3x}{2sin2x.cosx+2sin3x.cosx}=\frac{2cosx\left(cos2x+cos3x\right)}{2cosx\left(sin2x+sin3x\right)}\)
\(=\frac{cos2x+cos3x}{sin2x+sin3x}=\frac{2cos\frac{x}{2}.cos\frac{5x}{2}}{2sin\frac{5x}{2}.cos\frac{x}{2}}=cot\frac{5x}{2}\)
TH
9 tháng 8 2019
\(D=\frac{1+sin2x+cos2x}{1+sin2x-cos2x}=\frac{1+2sinxcosx+2cos^2x-1}{1+2sinxcosx-1+2sin^2x}\)
\(D=\frac{cosx\left(sinx+cosx\right)}{sinx\left(sinx+cosx\right)}=cotx\)
PN
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2019
\(A=\frac{sinx+sin3x+sin2x}{cosx+cos3x+cos2x}=\frac{2sin2x.cosx+sin2x}{2cos2x.cosx+cos2x}=\frac{sin2x\left(2cosx+1\right)}{cos2x\left(2cosx+1\right)}=\frac{sin2x}{cos2x}=tan2x\)
PU
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2021
\(A=\dfrac{sinx+sin3x+sin2x}{cosx+cos3x+cos2x}=\dfrac{2sin2x.cosx+sin2x}{2cos2x.cosx+cos2x}=\dfrac{sin2x\left(2cosx+1\right)}{cos2x\left(2cosx+1\right)}=tan2x\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 5 2020
\(A=\frac{sin3x-sinx+cos2x}{cosx-cos3x+sin2x}=\frac{2cos2x.sinx+cos2x}{2sin2x.sinx+sin2x}=\frac{cos2x\left(2sinx+1\right)}{sin2x\left(2sinx+1\right)}=\frac{cos2x}{sin2x}=cot2x\)
AH
Akai Haruma
Giáo viên
28 tháng 10 2023
Lời giải:
$A=\cos 2x-2\sin 5x\sin x=\cos 2x-2.\frac{-1}{2}[\cos (5x+x)-\cos (5x-x)]$
$=\cos 2x+\cos 6x-\cos 4x$
$=(\cos 2x+\cos 6x)-\cos 4x$
$=2\cos \frac{2x+6x}{2}\cos \frac{6x-2x}{2}-\cos 4x$
$=2\cos 4x\cos 2x-\cos 4x$
$=\cos 4x[2\cos 2x-1]$
Những đáp án A,B,C,D bạn đưa ra không có đáp án nào đúng cả.
28 tháng 10 2023
Mình cảm ơn bạn nhiều ạ! Mình cũng làm ra như vậy mà biến đổi mãi không sao ra.
\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x-\left(\dfrac{1}{2}sin4x-\dfrac{1}{2}sin2x\right)\)
\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin4x\)
\(=cos5x.sinx\)
gt rõ hơn được không ạ, e k hiểu lắm ạ