Ai giúp mình 2 giải bài này với minh cần gấp:
Bài 1: Cho tam giác ABC vuông ở A, phân giác BE. Kẻ EH vuông góc với BC (H thuộc BC) .Gọi K là giao điểm của AB va HE. Chứng minh rằng;
a, BE là đường trung trực của AH
b, EK=EC
c, AE<EC
BÀi 2: Cho đa thức; Q=x17 _ 1997x6 + 1997x15- 1997x14+...+ 1997x -1

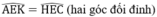
Bài 1:
Xét \(\Delta AEBvs\Delta HEB\)
BE cạnh huyền chung
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
\(\Delta AEB=\Delta HEB\)( cạnh huyền- góc nhọn)
\(\Rightarrow AB=HB;AE=EH\)( Các cặp cạnh tương ứng)
=> BE là đường trung trực của AH do(\(AB=HB;AE=EH\))
b) Xét\(\Delta AEKvs\Delta HEC\)
AE=EH( cmt)
\(\widehat{EAK}=\widehat{EHC}=90^0\)
\(\widehat{KEA}=\widehat{CEH}\)(đối đỉnh)
\(\Delta AEK=\Delta HEC\)(g-c-g)
=>EK=EC cặp cạnh tương ứng
c) Theo kết quả câu a ta đã có EA=EH
Trong tam giác vuông EHC có EH<EC
Nên EA< EC hay AE<EC
hình vẽ không được chính xác nhe bạn
Bài 2 đề yêu cầu làm gì vậy bạn?
bài 2 la f tính giá trị của đa thức Q tại x= 1996