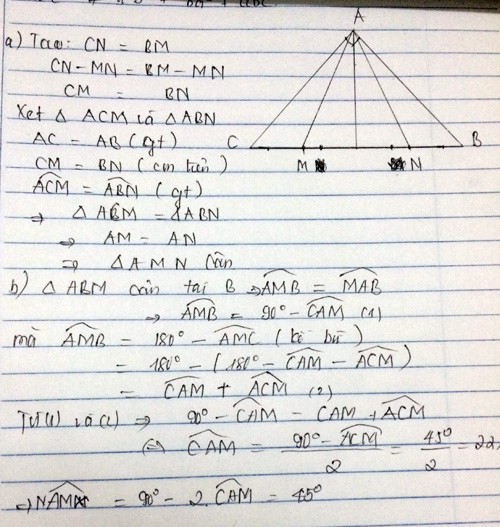
Cho tam giác ABC vuông tại A , trên cạnh BC lấy các điểm M,N sao cho BM=BA,CN=CA . Tính góc NAM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
1
MC
26 tháng 1 2019
Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)
NT
5 tháng 8 2016
xet tam giac ABM can tai B co ^A1= ^BAM - ^A2
va ^M1= \(\frac{180-B}{2}\); ^BAM= ^M1
xet tam giac ACN can tai C co ^A3= ^NAC - ^A2
va ^N1=\(\frac{180-C}{2}\); ^NAC= ^N1
ta co ^A1 + ^ A2 + ^ A3 =90
^A2+ ^BAM - ^A2 +^NAC - ^A2 =90
^N1 + ^M1 =90+ ^A2
\(\frac{180-B}{2}\)+\(\frac{180-C}{2}\)=90+ ^A2
\(\frac{360-\left(B+C\right)}{2}=90+A2\)
\(\frac{360-90}{2}=90+A2\)
=> ^A2=45
DD
0
TC
Thầy Cao Đô
Giáo viên
VIP
3 tháng 1 2023
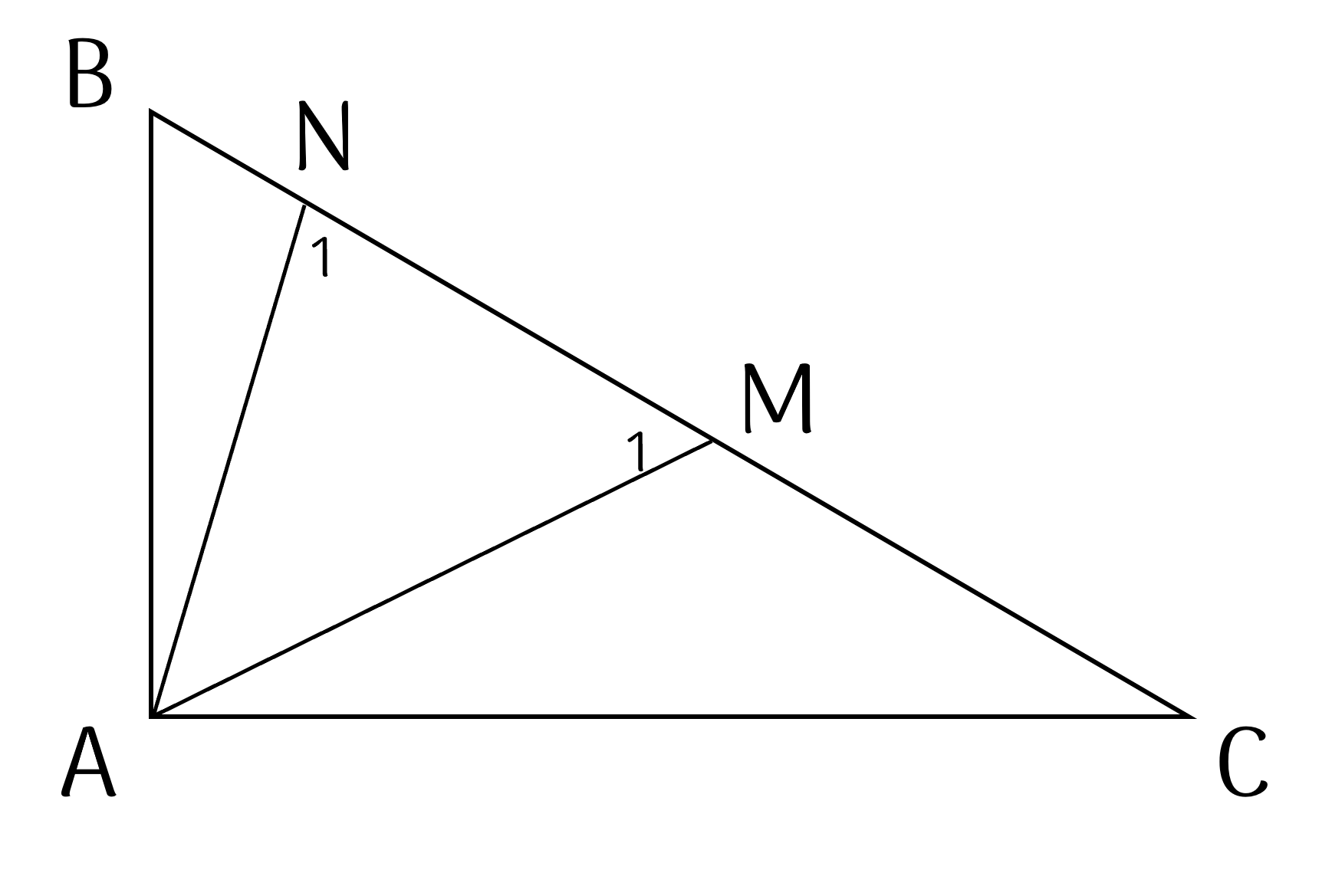
$BM = BA$ nên $\Delta BAM$ cân tại $B$.
Suy ra $\widehat{M_1} = \dfrac{180^{\circ} - \widehat{B}}2$.
$CN = CA$ nên $\Delta CAN$ cân tại $C$.
Suy ra $\widehat{N_1} = \dfrac{180^{\circ} - \widehat{C}}2$.
Suy ra $\widehat{N_1} + \widehat{M_1} = 180^{\circ} - \dfrac12(\widehat{B} + \widehat{C})$
nên $180^{\circ} - \widehat{N_1} - \widehat{M_1} = \dfrac12(\widehat{B} + \widehat{C})$
Trong $\Delta MAN$ có $\widehat{MAN} = 180^{\circ} - \widehat{N_1} - \widehat{M_1}$
nên $\widehat{MAN} = \dfrac12(\widehat{B} + \widehat{C}) = \dfrac12.90^{\circ} = 45^{\circ}$.
LK
0
DT
1
24 tháng 2 2021
Tam giác BAM cân tại B ( BM=BA ); tam giác CAN cân tại C => Góc AMN = (180 độ - B):2; Góc ANM = (180-C):2
Góc AMN + Góc CAN = (360-(B+C))/2=(360-90)/2=135
Xét tam giác AMN có góc MAN = 180 - ( Góc AMN + Góc CAN) = 180 -135 =45
Chúc bạn học giỏi ;)