tìm các số nguyên x và y
a, x/3 = 4/y
b, x/y =2/7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
2
15 tháng 1 2022
a: \(\left(x,y\right)\in\left\{\left(-9;1\right);\left(-1;9\right);\left(-3;3\right)\right\}\)
b: \(\left(x,y\right)\in\left\{\left(1;7\right);\left(-7;-1\right)\right\}\)
c: \(\left(x,y\right)\in\left\{\left(11;-1\right);\left(-11;1\right)\right\}\)
NK
1
15 tháng 1 2022
a: \(\left(x,y\right)\in\left\{\left(-9;1\right);\left(-1;9\right);\left(-3;3\right)\right\}\)
b: \(\left(x,y\right)\in\left\{\left(1;7\right);\left(-7;-1\right)\right\}\)
c: \(\left(x,y\right)\in\left\{\left(11;-1\right);\left(-1;11\right)\right\}\)
CM
17 tháng 3 2019
Đáp án D
Xét phương trình hoành độ giao điểm
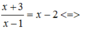
x2 – 4x – 1 = 0
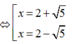
Giả sử A(2 + 5 ; 5 ); B(2 - 5 ; - 5 ) => yA + yB = 0
CM
30 tháng 10 2019
Đáp án D
Phương trình hoành độ giao điểm
x 3 − x + 3 = 2 x + 1 ⇔ x 3 − 3 x + 2 = 0
⇔ x − 1 2 x + 2 = 0 ⇔ x = − 2 x = 1
Do x A > x B nên x A = 1, x B = − 2 → y B = 2 − 2 + 1 = − 3
Vậy x B + y B = − 2 + − 3 = − 5
MN
20 tháng 2 2021
\(a.\)
\(\dfrac{x}{2}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{35}{7}=5\)
\(\Rightarrow x=5\cdot2=10\\ y=5\cdot5=25\)
\(b.\)
\(\dfrac{x+2}{y+10}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x+2}{1}=\dfrac{y+10}{5}\)
\(\Leftrightarrow\dfrac{3x+6}{3}=\dfrac{y+10}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\Leftrightarrow\dfrac{3x+6}{3}=\dfrac{y+10}{5}=\dfrac{y+10-3x-6}{5-3}=\dfrac{2-4}{2}=-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+6=-3\\y+10=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-15\end{matrix}\right.\)
\(c.\)
\(\dfrac{x}{4}=\dfrac{y}{5}\)
\(\Leftrightarrow\dfrac{2x}{8}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{15}{3}=5\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=5\cdot8\\y=5\cdot5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\)
20 tháng 2 2021
a) Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=35
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{35}{7}=5\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=5\\\dfrac{y}{5}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=25\end{matrix}\right.\)
Vậy: (x,y)=(10;25)
b) Ta có: \(\dfrac{x+2}{y+10}=\dfrac{1}{5}\)
nên \(\dfrac{x+2}{1}=\dfrac{y+10}{5}\)
hay \(\dfrac{3x+6}{3}=\dfrac{y+10}{5}\)
mà y-3x=2
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x+6}{3}=\dfrac{y+10}{5}=\dfrac{y-3x+10-6}{5-3}=\dfrac{2+4}{2}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{3x+6}{3}=3\\\dfrac{y+10}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6=9\\y+10=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(1;5)
c) Ta có: \(\dfrac{x}{4}=\dfrac{y}{5}\)
nên \(\dfrac{2x}{8}=\dfrac{y}{5}\)
mà 2x-y=15
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{15}{3}=5\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{4}=5\\\dfrac{y}{5}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\)
Vậy: (x,y)=(20;25)
5 tháng 6 2021
Giải:
a) \(y^2=3-\left|2x-3\right|\)
Vì \(-\left|2x-3\right|\le0\forall x\) nên \(3-\left|2x-3\right|\le3\forall x\) nên \(y^2\le3\rightarrow y^2\in\left\{0;1\right\}\) (vì \(y\in Z\) )
TH1:
\(y^2=0\)
\(\Rightarrow y=0\)
\(\Rightarrow\left|2x-3\right|=3\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
TH2:
\(y^2=1\)
\(\Rightarrow y=\pm1\)
NN
2
26 tháng 11 2023
a: xy=x-y
=>xy-x+y=0
=>xy-x+y-1=-1
=>x(y-1)+(y-1)=-1
=>(x+1)(y-1)=-1
=>\(\left(x+1\right)\left(y-1\right)=1\cdot\left(-1\right)=\left(-1\right)\cdot1\)
=>\(\left(x+1;y-1\right)\in\left\{\left(1;-1\right);\left(-1;1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;0\right);\left(-2;2\right)\right\}\)
b: x(y+2)+y=1
=>\(x\left(y+2\right)+y+2=3\)
=>\(\left(x+1\right)\left(y+2\right)=3\)
=>\(\left(x+1\right)\cdot\left(y+2\right)=1\cdot3=3\cdot1=\left(-1\right)\left(-3\right)=\left(-3\right)\left(-1\right)\)
=>\(\left(x+1;y+2\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;1\right);\left(2;-1\right);\left(-2;-5\right);\left(-4;-3\right)\right\}\)
25 tháng 2 2022
\(\dfrac{x}{3}=\dfrac{y}{7}\Rightarrow\)\(\dfrac{x}{3}\times\dfrac{y}{7}=\dfrac{xy}{21}=\left(\dfrac{x}{3}\right)^2=\left(\dfrac{y}{7}\right)^2\)
\(\dfrac{xy}{21}=\dfrac{84}{21}=4\)
\(\Rightarrow\left(\dfrac{x}{3}\right)^2=4\Rightarrow\)\(\dfrac{x}{3}=2\Rightarrow x=6\)
\(\Rightarrow\left(\dfrac{y}{7}\right)^2=4\Rightarrow\)\(\dfrac{y}{7}=2\Rightarrow y=14\)
x/3=y/4
<=> x/y=4/3
<=> x=4k; y=3k
x/y=2/7
<=> x=2k; y=7k