x2+7x-ạ^2+a+12=0 với a là hằng số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(x^2+7x-a^2+a+12=0\)
\(\Leftrightarrow x^2-ax+4x+ax+3x-a^2+a+12=0\)
\(\Leftrightarrow\left(x^2-ax+4x\right)+\left(ax+3x\right)-\left(a^2+3a\right)+\left(4a+12\right)=0\)
\(\Leftrightarrow x\left(x-a+4\right)+x\left(a+3\right)-a\left(a+3\right)+4\left(a+3\right)=0\)
\(\Leftrightarrow x\left(x-a+4\right)+\left(a+3\right)\left(x-a+4\right)=0\)
\(\Leftrightarrow\left(x+a+3\right)\left(x-a+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+a+3=0\\x-a+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-a-3\\x=a-4\end{cases}}}\)
Vậy \(x=-a-3\) hoặc \(x=a-4\)

Bài 1)1)\(x^2+5x+6=x^2+3x+2x+6\)=0
=x(x+3)+2(x+3)=(x+2)(x+3)=0
Dễ rồi
2)\(x^2-x-6=0=x^2-3x+2x-6=0\)
=x(x-3)+2(x-3)=0
=(x+2)(x-3)=0
Dễ rồi
3)Phương trình tương đương:\(\left(x^2+1\right)\left(x+2\right)^2=0\)
Vì \(x^2+1>0\)
=>\(\left(x+2\right)^2=0\)
Dễ rồi
4)Phương trình tương đương\(x^2\left(x+1\right)+\left(x+1\right)\)=0
=> \(\left(x^2+1\right)\left(x+1\right)=0Vì\) \(x^2+1>0\)
=>x+1=0
=>..................
5)\(x^2-7x+6=x^2-6x-x+6\) =0
=x(x-6)-(x-6)=0
=(x-1)(x-6)=0
=>.....
6)\(2x^2-3x-5=2x^2+2x-5x-5\)=0
=2x(x+1)-5(x+1)=0
=(2x-5)(x+1)=0
7)\(x^2-3x+4x-12\)=x(x-3)+4(x-3)=(x+4)(x-3)=0
Dễ rồi
Nghỉ đã hôm sau làm mệt

Để olm giúp em em nhé!
a, \(\dfrac{x+2}{7x+42}\) = \(\dfrac{x+2}{7.\left(x+6\right)}\) = \(\dfrac{\left(x+2\right)\left(x-6\right)}{7\left(x-6\right)\left(x+6\right)}\) (đk \(x\ne\) \(\mp\) 6)
\(\dfrac{-13x}{x^2-36}\) = \(\dfrac{-13x}{\left(x-6\right)\left(x+6\right)}\) = \(\dfrac{-7.13.x}{7.\left(x-6\right).\left(x+6\right)}\) = \(\dfrac{-91x}{7.\left(x-6\right)\left(x+6\right)}\)
b, \(\dfrac{7}{4x+16}\) = \(\dfrac{7\left(x-4\right)}{4.\left(x+4\right).\left(x-4\right)}\) (đk \(x\ne\) \(\pm\) 4)
\(\dfrac{15}{x^2-16}\) = \(\dfrac{15.4}{\left(x-4\right)\left(x+4\right).4}\) = \(\dfrac{60}{4.\left(x-4\right).\left(x+4\right)}\)

a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
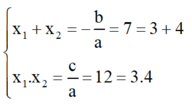
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
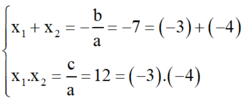
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

Ta có T = (x + 2)(x + 3)(x + 4)(x + 5) – 24
= [(x + 2)(x + 5)].[(x + 3)(x + 4)] – 24
= ( x 2 + 7x + 10).( x 2 + 7x + 12) – 24
Đặt x 2 + 7x + 11= t, ta được
T = (t – 1)(t + 1) – 24 = t 2 – 1 – 24 = t 2 – 25 = (t – 5)(t + 5)
Thay t = x 2 + 7x + 11, ta được
T = (t – 5)(t + 5) = ( x 2 + 7x + 11 – 5)( x 2 + 7x + 11 + 5)
= ( x 2 + 7x + 6)( x 2 + 7x + 16)
Suy ra a = 6; b = 16 => a – b = -10
Đáp án cần chọn là: D




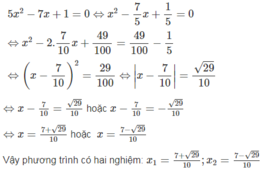
=(x2+7x+12)-a2+a=0
=(x+3)(x+4)-a2+a=0
Đặt x+3=y.Ta có
=y2+y-a2+a=0
=(y-a+1)(y+a)=0
=>y=a-1,y=-a
mà x+3=y
=>x=a-4 và x=-a-3