Hướng dẫn giải của bài toán này:
x.y.z = a,x .y = b,x + z = c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2016
Ta phải giả sử x,y,z khác 0
gt: (yc-bz)/x=(za-xc)/y =>
(c/z-b/y)/zx^2=(a/x-c/z)/zy^2 hay:
(c/z-b/y)/x^2=(a/x-c/z)/y^2 (*)
mặt khác từ gt:
(yc-bz)/x=(xb-ya)/z =>
(c/z-b/y)/yx^2=(b/y-a/x)/yz^2 hay:
(c/z-b/y)/x^2=(b/y-a/x)/z^2 (**)
*nếu: c/z-b/y>0
<=>c/z>b/y
Theo (*) ta có:
a/x-c/z>0
<=>a/x>c/z
=>a/x>c/z>b/y
=>b/y-a/x<0 vô lí vì từ (**) :
b/y-a/x>0
*nếu: c/z-b/y<0
<=>c/z<b/y
Theo (*) ta có:
a/x-c/z<0
=>a/x<c/z
=>a/x<c/z<b/y.
=>b/y-a/x>0. vô lí vì theo (**) => b/y-a/x<0
Vậy ta phải có:
c/z-b/y=0
Thay vào (*) ta có:
a/x=b/y=c/z.
LM
17 tháng 7 2016
x/y=y/z=z/x
=> x*z = 2*y = x*y = 2*z
Ta có :
x*z = x*y
=> z=y
Ta có :
x*z = 2*y = y*y
Mà y = z (cmt)
=> x*z = y*z
=>x=y
Mà y = z (cmt)
=> x=y=z
LC
1
HT
18 tháng 6 2016
Từ \(a+b+c=0\Rightarrow a+b=-c\)
Xét hiệu \(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)\left(I\right)\)
Thay \(a+b=-c;a+b+c=0\left(GT\right)v\text{ào}\left(I\right)\) ta được
\(a^3+b^3+c^3-3abc=\left(-c\right)^3+c^3-3ab.0\)
\(=0\)
\(\Rightarrow a^3+b^3+c^3=3abc\left(\text{Đ}PCM\right)\)
Vậy \(a^3+b^3+c^3=3abc\) với \(a+c+b=0\)
CM
5 tháng 8 2017
Theo đề bài ta có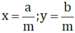 
(a, b, m ∈ Z; m > 0).
Quy đồng mẫu số các phân số ta được: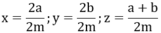 
Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.
Vì a < b nên a + a < b + a hay 2a < a + b.
Vì a < b nên a + b < b + b hay a + b < 2b.
Vậy ta có 2a < a+b < 2b nên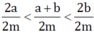 
hay x < z < y.
29 tháng 8 2016
Chứng tỏ rằng nếu \(z=\frac{a+b}{2.m}\) thì ta x < z < y.
Ta có:
\(x=\frac{am}{2m};y=\frac{bm}{2m}\)
Vì x < y cho nên:
=> am < bm => am + am < am + b => a (2m) < b (a.b)
=> \(\frac{a}{m}< \frac{a+b}{2m}\)
Cũng tương tự như vậy ta có: \(\frac{a+b}{2m}< \frac{b}{m}\)
Do đó: \(\frac{a}{m}< \frac{a+b}{2m}< \frac{b}{m}\)
TM
27 tháng 12 2016
Đặt \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=k\Rightarrow\hept{\begin{cases}x=ak\\y=bk\\z=ck\end{cases}}\)
=>\(B=\frac{\left(a^2x+b^2y+c^2z\right)^3}{x^3+y^3+z^3}=\frac{\left(a^2ak+b^2bk+c^2ck\right)^3}{\left(ak\right)^3+\left(bk\right)^3+\left(ck\right)^3}=\frac{\left(a^3k+b^3k+c^3k\right)^3}{a^3k^3+b^3k^3+c^3k^3}\)
\(=\frac{k^3\left(a^3+b^3+c^3\right)^3}{k^3\left(a^3+b^3+c^3\right)}=\left(a^3+b^3+c^3\right)^2\)
28 tháng 12 2016
cảm ơn trà my nhiều
bài nè ko phải gửi đi lấy điểm đâu các bn.