Cho x+y+z=3,0=<x,y,z=<2 . Tìm GTLN của biểu thức A=x^2+y^2+z^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(B=\dfrac{\left(x+y\right)^2-z^2}{x+y+z}\)
\(=\dfrac{\left(x+y-z\right)\left(x+y+z\right)}{x+y+z}\)
=x+y-z
c:
ĐKXĐ: x<>1
\(C=\dfrac{x^2-6x+5}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)\left(x-5\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x-5}{x-1}\)

Gọi công thức X, Y ,Z dạng CxHyOz vơi x, y, z nguyên dương Ta có: 12x + y + 16z = 82 vơi Z nhỏ hơn hoặc = 4
Xet các trường hợp:
Z =1 => x = 5, y = 6
=> CTPT là C5H6O
Z = 2 => x = 4 và y = 2
=> CTPT C4H2O2
Vơi Z = 3,4 , không có ctpt thỏa man
Theo bài ra, 1 mol Y tác dụng vơi 4 mol AgNO3 nên Y phải có 2 nhóm CHO => Y là OHC-C C-CHO
Theo bài ra, 1 mol X hoặc Z tác dung vơi 3 mol AgNO3 chứng tỏ X và Z phải có 1 nhóm CHO và 1 liên kết 3 ở đầu mach, đồng thời X và Y đồng phân nên
X: CH C-CO-CHO
Z: HC C-CH2CH2CHO
Tơi đây, ta có kết luận không đúng là B
=> Đáp án B

Đáp án C.
![]()
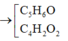
+ 1 mol Y tác dụng vừa đủ với dung dịch chứa 4 mol AgNO3/NH3, đun nóng → Y = OHC-C≡C-CHO.
+ X và Y là đồng phân của nhau và 1 mol X tác dụng vừa đủ với dung dịch chứa 3 mol AgNO3/NH3, đun nóng → X = CH≡C-CO-CHO.
+ 1 mol Z tác dụng vừa đủ với dung dịch chứa 3 mol AgNO3/NH3, đun nóng → Z = CH≡CCH2CH2CHO.
→ D sai, phần trăm khối lượng H trong X và Z lần lượt là 2,44% và 7,32%.

Đáp án C.
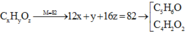
+ 1 mol Y tác dụng vừa đủ với dung dịch chứa 4 mol AgNO3/NH3, đun nóng → Y = OHC-C≡C-CHO.
+ X và Y là đồng phân của nhau và 1 mol X tác dụng vừa đủ với dung dịch chứa 3 mol AgNO3/NH3, đun nóng → X = CH≡C-CO-CHO.
+ 1 mol Z tác dụng vừa đủ với dung dịch chứa 3 mol AgNO3/NH3, đun nóng → Z = CH≡CCH2CH2CHO.
→ D sai, phần trăm khối lượng H trong X và Z lần lượt là 2,44% và 7,32%.

Đáp án B
Z là chất lỏng ở điều kiện thường, tan vô hạn trong nước nên Z là ancol etylic.
X là chất rắn ở điều kiện thường, tan ít trong nước lạnh, tan nhiều trong nước nóng nên X là phenol.
Còn lại Y là anilin.

Đáp án C
![]()
CO2 + dung dịch NaOH
NaOH + CO2 → NaHCO3 (1)
2NaOH + CO2 → Na2CO3 + H2O (2)
BaCl2
+ Na2CO3 → BaCO3↓ + 2NaCl
![]()
![]()
Dung dịch Z + dung dịch KOH
2NaHCO3 + 2KOH → K2CO3 + Na2CO3 + 2H2O
![]()
![]()
![]()
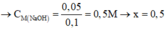
![]()
Từ phương trình (*) → m M g C O 3 p h ả n ứ n g = 0,03.84 = 2,52 g
→ Hiệu suất phản ứng là:
![]()
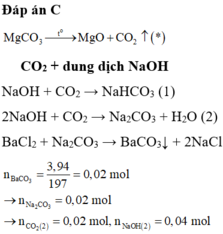
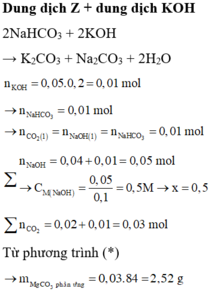

Áp dụng BĐT Bunhiacopski ta có:
\(\left(1^2+1^2+1^2\right)\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)
\(\Rightarrow3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2=3^2=9\)
\(\Rightarrow x^2+y^2+z^2\ge3\Rightarrow A\ge3\)
Dấu "=" xảy ra khi x=y=z=1
Vậy MinA=3 khi x=y=z=1
(Bạn Thắng Nguyễn, đề yêu cầu tìm \(max\) mà...)
Đây là bài bất đẳng thức khó, vì \(maxA=5\) và đẳng thức xảy ra tại \(x=0,y=1,z=2\) (chẳng có BĐT nào làm được hết).
Lời giải đây: Đặt \(A=f\left(x,y,z\right)=x^2+y^2+z^2\) (coi như đa thức 3 biến)
Trong \(x,y,z\) phải có số lớn hơn hoặc bằng 1, giả sử là \(x\). Khi đó \(y+z\le2\).
\(f\left(x,y+z,0\right)=x^2+\left(y+z\right)^2\ge x^2+y^2+z^2=f\left(x,y,z\right)\)
Mà \(f\left(x,y+z,0\right)=f\left(x,3-x,0\right)=x^2+\left(3-x\right)^2=2x^2-6x+9\)
Và biểu thức này đạt giá trị lớn nhất tại \(x=2\) (giải thích: \(2x^2-6x+9=2\left|x-\frac{3}{2}\right|^2+\frac{9}{2}\))
Nên \(f\left(x,y,z\right)\le f\left(2,1,0\right)=5\). Đẳng thức xảy ra tại \(x=2,y=1,z=0\).