Cho hàm số y= x+1/ 2x-1 , có đồ thị (H). Gọi A (x1,y1), B(x2,y2) là hai điểm phân biệt thuộc (H) sao cho tiếp tuyến của ( H) tại A,B có cùng hệ số góc k. Tìm k biết diện tích tam giác OAB bằng 1/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Đạo hàm : y’ = 4/3.x3-28/3. x
y 2 - y 1 = 8 ( x 2 - x 1 ) ⇔ y 2 - y 1 x 2 - x 1 = 8
Vậy tiếp tuyến của (C) tại A có hệ số góc bằng 8.
+ Xét phương trình y' = 8
⇔ 4 3 x 3 - 28 3 x = 8 ⇔ 4 x 3 - 28 x - 24 = 0
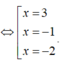
+) Với x= 3 thì A( 3; -15) nên phương trình tiếp tuyến của (C) tại A là y = 8(x-3) - 15 ( d 1 )
Phương trình hoành độ giao điểm của (C) và ( d 1 ) là
8 ( x - 3 ) - 15 = 1 3 x 4 - 14 3 x 2 ⇔ ( x - 3 ) 2 ( x 2 + 6 x + 13 ) = 0 ⇔ x = 3 .
Vậy A(3; -15) loại.
+) Với x= -2 thì A(-2; -40/3) . phương trình tiếp tuyến của (C) tại A là y = 8(x+2) - 40/3 ( d 2 )
Phương trình hoành độ giao điểm của ( C) và ( d 2 ) là
8 ( x + 2 ) - 40 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 4 x - 2 ) = 0
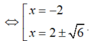
Vậy A( -2; -40/3) thỏa mãn.
+) Với x= -1 thì A( -2; -13/ 3) nên phương trình tiếp tuyến của C tại A là
y = 8(x+1) - 13/3 (d3)
Phương trình hoành độ giao điểm của C và (d3) là:
8 ( x + 1 ) - 13 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 2 x - 11 ) = 0

Vậy A( -1; -13/3) thỏa mãn.
Vậy có tất cả 2 điểm A thỏa mãn yêu cầu bài toán.
Chọn B.

Theo mình không tìm được cụ thể a,b đâu, bởi nó còn thiếu 1 pt nữa
\(A\left(a;a^3-3a^2+2a+1\right);B\left(b;b^3-3b^2+2b+1\right)\)
\(k_A=k_B\Leftrightarrow y'\left(a\right)=y'\left(B\right)\Leftrightarrow3a^2-6a+2=3b^2-6b+2\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)-2\left(a-b\right)=0\Leftrightarrow\left(a-b\right)\left(a+b-2\right)=0\Leftrightarrow\left[{}\begin{matrix}a=b\left(loai\right)\\a+b=2\end{matrix}\right.\)

Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 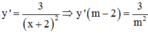
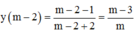
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 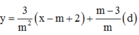
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
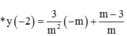
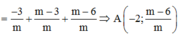
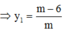
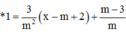
![]()
![]()
![]()
![]()
![]()
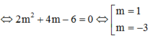
![]()

Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
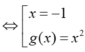
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.

Ý tưởng thế này: tọa độ A, B thỏa mãn:
\(\left\{{}\begin{matrix}6x^2+6ax=6\\y=2x^3+3ax^2+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2=1-ax\\y=2x^3+3ax^2+b\end{matrix}\right.\)
\(\Rightarrow y=2x\left(1-ax\right)+3a\left(1-ax\right)+b\)
\(\Rightarrow y=-2ax^2+2x-3a^2x+3a+b\)
\(\Rightarrow y=-2a\left(1-ax\right)+2x-3a^2x+3a+b\)
\(\Rightarrow y=\left(2-a^2\right)x+a+b\)
\(\Rightarrow\left(2-a^2\right)x-y+a+b=0\)
Đây chính là pt AB theo a;b
Từ khoảng cách \(\Rightarrow\dfrac{\left|a+b\right|}{\sqrt{\left(2-a^2\right)^2+1}}=1\Leftrightarrow\left(a+b\right)^2=\left(2-a^2\right)^2+1\)
\(\Leftrightarrow\left(a+b\right)^2=a^4-4a^2+5\)
\(\Leftrightarrow2a^2+\left(a+b\right)^2=a^4-2a^2+5=\left(a^2-1\right)^2+4\ge4\)
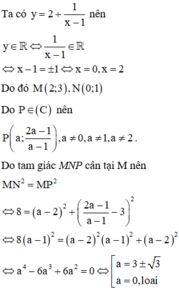
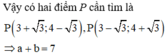
\(y'=\dfrac{-3}{\left(2x-1\right)^2}\)
Tiếp tuyến tại A và B cùng hệ số góc
\(\Leftrightarrow\dfrac{-3}{\left(2x_A-1\right)^2}=\dfrac{-3}{\left(2x_B-1\right)^2}\Leftrightarrow\left(2x_A-1\right)^2-\left(2x_B-1\right)^2=0\)
\(\Leftrightarrow\left(x_A-x_B\right)\left(x_A+x_B-1\right)=0\)
\(\Leftrightarrow x_A+x_B=1\) (do A ; B phân biệt nên \(x_A-x_B\ne0\))
\(\Rightarrow x_B=1-x_A\)
Ta có: \(A\left(x_A;\dfrac{x_A+1}{2x_A-1}\right)\) ; \(B\left(1-x_A;\dfrac{x_A-2}{2x_A-1}\right)\)
\(S_{OAB}=\dfrac{1}{2}\left|\left(x_A-x_O\right)\left(y_B-y_O\right)-\left(x_B-x_O\right)\left(y_A-y_O\right)\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left|x_A\left(\dfrac{x_A-2}{2x_A-1}\right)-\left(1-x_A\right)\left(\dfrac{x_A+1}{2x_A-1}\right)\right|=1\)
\(\Leftrightarrow\left|\dfrac{2x_A^2-2x_A-1}{2x_A-1}\right|=1\) \(\Leftrightarrow\left[{}\begin{matrix}2x_A^2-2x_A-1=2x_A-1\\2x_A^2-2x_A-1=1-2x_A\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x_A^2-4x_A=0\\2x_A^2=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_A=0\\x_A=2\\x_A=1\\x_A=-1\end{matrix}\right.\) \(\Rightarrow k=...\)
Chỗ SOAB mình áp dụng công thức gì vậy ạ