Tính
(2m+3)(-1)-m+1=3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Rút gọn A = ( 5 m ) 2 = 25 m 2 . Với m = 2 Þ A = 100.
b) Rút gọn B = -12x + 26. Với x = 10 Þ B = -94.

a) 1 , 5 x 2 – 1 , 6 x + 0 , 1 = 0
Có a = 1,5; b = -1,6; c = 0,1
⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0
⇒ Phương trình có hai nghiệm x 1 = 1 ; x 2 = c / a = 1 / 15 .

d) ( m – 1 ) x 2 – ( 2 m + 3 ) x + m + 4 = 0
Có a = m – 1 ; b = - (2m + 3) ; c = m + 4
⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m -1 – 2m – 3 + m + 4 = 0
⇒ Phương trình có hai nghiệm 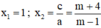

a) √(√3 - 2)² + √3
= 2 - √3 + √3
= 2
b) Để (d) và (d') cắt nhau thì:
m + 2 ≠ -2
m ≠ -2 - 2
m ≠ -4
Vậy m ≠ -4 thì (d) cắt (d')
c) Thay tọa độ điểm A(3; -1) vào (d) ta có:
(2m - 3).3 + m = -1
⇔ 6m - 9 + m = -1
⇔ 7m = -1 + 9
⇔ 7m = 8
⇔ m = 8/7 (nhận)
Thay m = 8/7 vào (d) ta có:
(d): y = -5x/7 - 8/7
Vậy hệ số góc của (d) là -5/7

a)
\(\dfrac{2-x}{2002}-1=\dfrac{1-x}{2003}-\dfrac{x}{2004}\)
\(\Leftrightarrow\dfrac{2-x}{2002}+1=\dfrac{1-x}{2003}+1+\dfrac{-x}{2004}+1\)
\(\Leftrightarrow\dfrac{2004-x}{2002}-\dfrac{2004-x}{2003}-\dfrac{2004-x}{2004}=0\)
\(\Leftrightarrow\left(2004-x\right)\left(\dfrac{1}{2002}-\dfrac{1}{2003}-\dfrac{1}{2004}\right)\)
\(\Leftrightarrow2004-x=0\) (vì \(\dfrac{1}{2002}-\dfrac{1}{2003}-\dfrac{1}{2004}\ne0\))
\(\Leftrightarrow x=2004\)
S={2004}

Cho đường thẳng (d): (y=(2m+1)x-2) với m là tham số và (m\ne-\frac{1}{2}.) Khoảng cách từ (A(-2;1)) đến đường thẳng d được tính theo công thức:
[\sqrt{(-2-(2m+1)(-2))^2+(1-(2m+1)(-2))^2}]
[\sqrt{(16m^2+20m+4)^2+(24m+4)^2}]
[\sqrt{256m^4+640m^3+320m^2+576m^2+960m+16}]
[\sqrt{256m^4+1216m^3+1536m^2+960m+16}]
[\sqrt{16m^2(16m^2+79m+96)+4(16m^2+79m+96)}]
[\sqrt{(4m+7)^2(4m+16)}]
Theo đề bài, khoảng cách này bằng (\frac{1}{\sqrt{2}}.) Do đó, ta có phương trình:
[\sqrt{(4m+7)^2(4m+16)}=\frac{1}{\sqrt{2}}]
Từ đây, ta được phương trình bậc hai:
[(4m+7)^2(4m+16)=1 ]
Giải phương trình này, ta được hai nghiệm:
[m=-\frac{3}{2}\pm\frac{\sqrt{3}}{2} ]
Do (m\ne-\frac{1}{2},) ta có nghiệm duy nhất là:
[m=-\frac{3}{2}+\frac{\sqrt{3}}{2}=\frac{5}{7} ]
Vậy, tổng các giá trị của m thỏa mãn bài toán là [\frac{5}{7}.]

a: \(\text{Δ}=\left(-5\right)^2-4\left(-2m+5\right)\)
=25+8m-20=8m+5
Để phương trình có nghiệm kép thì 8m+5=0
=>m=-5/8
=>x^2-5x+25/4=0
=>x=5/2
b: \(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2m+3\right)\)
\(=4m^2-4m+1-4m^2+8m-12=4m-11\)
Để phương trình có nghiệm kép thì 4m-11=0
=>m=11/4
=>x^2-9/2x+81/16=0
=>x=9/4
c: TH1: m=-3
=>-(2*(-3)+1)x+(-3-1)=0
=>-(-5x)-4=0
=>5x-4=0
=>x=4/5(nhận)
TH2: m<>-3
\(\text{Δ}=\left(2m+1\right)^2-4\left(m+3\right)\left(m-1\right)\)
\(=4m^2+4m+1-4\left(m^2+2m-3\right)\)
\(=4m^2+4m+1-4m^2-8m+12=-4m+13\)
Để phương trình có nghiệm kép thì -4m+13=0
=>m=13/4
=>25/4x^2-15/2x+9/4=0
=>(5/2x-3/2)^2=0
=>x=3/2:5/2=3/2*2/5=3/5
$(2m + 3)(-1) - m + 1 = 3$
$⇔ -2m - 3 - m + 1 = 3$
$⇔ -3m - 2 = 3$
$⇔ - 3m = 5$
$⇔ m = \dfrac{-5}{3}$
(2m+3)(-1) - m + 1 = 3
-2m - 3 - m + 1 = 3
-3m - 2 = 3
-3m = 5
m = - 5: 3
m = -5/3