Cho tam giác ABC (AB>AC), trung tuyến AM,trên tia đối của tia MA lấy điểm D sao cho MD= MA.
a. Chứng minh ABDC là hình bình hành
b.Gọi E là điểm đối xứng của A qua BC.Chứng minh BC song song với ED
c.Chứng minh BCDE là hình thang cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ABC vuông tại A (AB < AC), trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
AB tại E, HF
18 tháng 8 2022
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
b,d: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AFE=góc AHE=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc ACB
=>góc MAC+góc EFA=90 độ
=>AM vuông góc với EF
c: Xét ΔADI có
H,M lần lượt là trung điểm của AI và AD
nên HM là đường trung bình
=>HM//DI
=>DI//BC
Xét ΔCIA có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCIA cân tại C
=>CI=CA=DB
=>BIDC là hình thang cân
KV
12 tháng 12 2023
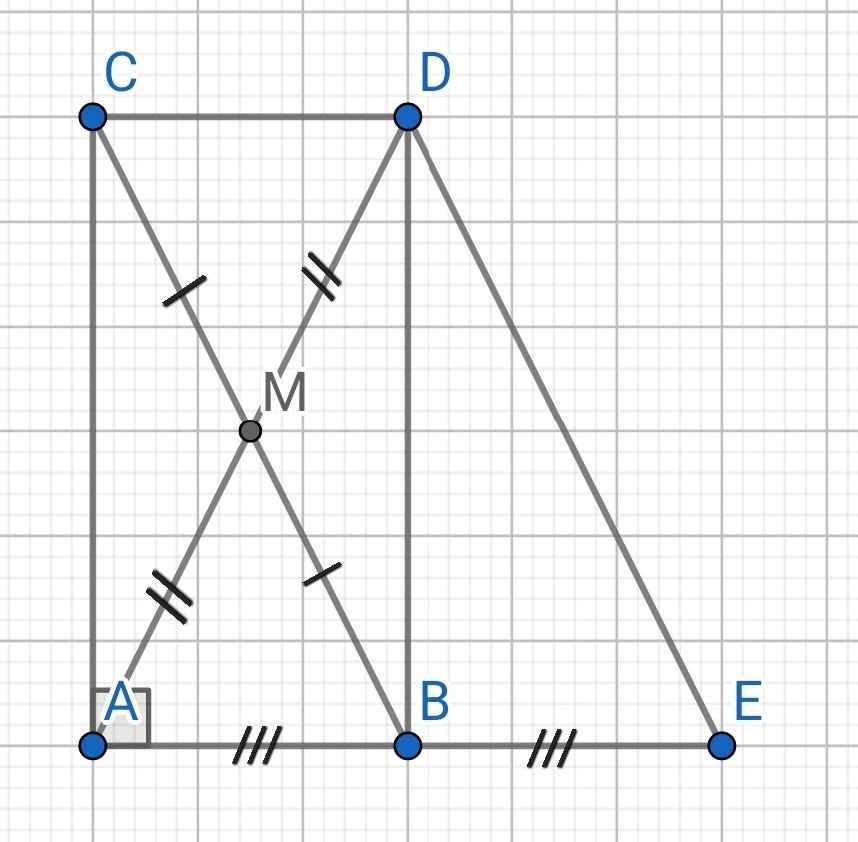a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!
MS
11 tháng 7 2023
a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành
CW
7 tháng 1 2017
a) chứng minh theo dấu hiệu: tứ giác 2 đường chéo cắt nhau tại trung điểm là hình bình hành (bạn tự cm nhé ^^!)
b) Kẻ BE. Gọi giao điểm của BM và AE là H
tam giác ABE có BH _|_ AE và HA=HE
=> tam giác ABE cân tại B hay AB = EB (1)
Mà AB = CD (do tứ giác ABDC là hbh) (2)
Từ (1) và (2) => CD = EB (*)
Tam giác EAD: HA=HE và MA=MD => HM // ED => tứ giác CBDE là hình thang (**)
Từ (*) và (**) => CBDE là hình thang cân
KL
2 tháng 1 2017
a) Chứng minh : ABCD là hình bình hành
Xét : Tứ giác ABCD có :
M trung điểm AD ( MD = MA (gt) ; M , D , A thẳng hàng )
M trung điểm BC ( AM trung tuyến của tam giác ABC (gt) )
Vậy ABCD là hình bình hành (đpcm)
b) Chứng minh : BC song song ED
Gọi I là giao điểm của AE với BC
Xét : Tam giác AED có :
M trung điểm BC ( cmt )
I trung điểm AE ( A đối xứng E qua BC (gt) => BC trung trực AE , AE cắt BC tại I )
Vậy BI là đường trung bình của tam giác AED
=> MI song song ED
Mà : MI thuộc BC
Nên : BC song song ED ( đpcm )
c) Chứng minh : BCDE là hình thang cân
Ta có :
. BC song song ED ( cmt )
=> Hình thang BCDE (1)
. Góc IBA = góc BCD ( AB song song CD ( hình bình hành ABCD ))
. A đối xứng với E qua BC (gt) => BC trung trực AE => BA = BE => Tam giác AEB cân tại B => BI là trung trực AE đồng thời là phân giác của tam giác AEB => Góc CBE = góc IBA
Vậy góc CBE = góc BCD ( = góc IBA ) (2)
Từ (1) và (2) =.> Hình thang cân BCDE ( đpcm)
29 tháng 12 2021
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật
29 tháng 12 2021
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật