giải phương trình : x4 - 3x3 - 6x + 4 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
PT
1
CM
16 tháng 12 2019
Đặt f(x) = x4 - 3x3 + x – 1.
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(0) = -1 < 0
f(-1) = 1 – 3.(-1) – 1 – 1 = 2 > 0
⇒ f(0).f(-1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm xo ∈ (-1; 0) ⊂ (-1 ; 3).
Do đó phương trình đã cho có nghiệm xo ∈ (-1; 3).
HN
0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
PT
1
CM
13 tháng 3 2018
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
PT
1
CM
30 tháng 9 2017
x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
22 tháng 12 2021
\(x^4-3x-4=0\\ x^4+x-4x-4=0\\ x^3\left(x+1\right)-4\left(x+1\right)=0\\ \left(x^3-4\right)\left(x+1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x^3-4=0\Leftrightarrow x^3=4\Leftrightarrow x=\sqrt[3]{4}\\x+1=0\Leftrightarrow x=-1\end{matrix}\right.\)
TC
11 tháng 1 2023
`x^4 -4sqr{3} -5 =0`
`<=> x^4 = 5 +4sqrt{3}`
`<=> x = +- root{4}{5+4sqrt(3)}`
Vậy `S ={ +- root{4}{5+4sqrt(3)} }`
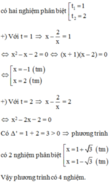
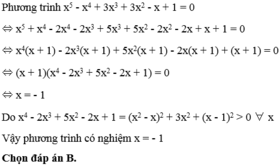
\(x^4-3x^3-6x+4=0\)
<=>\(\left(x^4+x^3+2x^2\right)-\left(4x^3+4x^2+8x\right)+\left(2x^2+2x+4\right)=0\)
<=>\(x^2\left(x^2+x+2\right)-4x\left(x^2+x+2\right)+2\left(x^2+x+2\right)=0\)
<=>\(\left(x^2+x+2\right)\left(x^2-4x+2\right)=0\)<=>\(\orbr{\begin{cases}x^2+x+2=0\\x^2-4x+2=0\end{cases}}\)
+)\(x^2+x+2=0\)
\(x^2+x+2=x^2+2.\frac{1}{2}.x+\frac{1}{4}+\frac{7}{4}=\left(x+\frac{1}{4}\right)^2+\frac{7}{4}\ge\frac{7}{4}>0\)
=> ko có x thỏa mãn x2+x+2=0
+)\(x^2-4x+2=0\)
\(x^2-4x+2=x^2-4x+4-2=\left(x-2\right)^2-2=0\)
<=>\(\left(x-2\right)^2=2\)<=>\(\orbr{\begin{cases}x-2=\sqrt{2}\\x-2=-\sqrt{2}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\sqrt{2}+2\\x=2-\sqrt{2}\end{cases}}\)
Vậy tập nghiệm pt \(S=\left\{2-\sqrt{2};\sqrt{2}+2\right\}\)