Tìm các số tự nhiên a và b sao cho : ab + 2b = 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
7 tháng 11 2021
(3a+2b).8+10a+b=24a+16a+10a+b=34a+17b chia hết cho 17
⇒(3a+2b).8+10a+b chia hết cho 17
Mà 3a+2b chia hết cho 17⇒(3a+2b).8 chia hết cho 17
⇒10a+b chia hết cho 17(đpcm)
b)Ta có :
xy+x-y=4
⇒x.(y+1)-(y+1)=3
⇒(x-1).(y+1)=3
Vì x,y ∈Z
⇒x-1,y+1∈Z
⇒x-1,y+1∈Ư(3)
Lập bảng giá trị
x -1 1 3 -1 -3
y+1 3 1 -3 -1
x 2 4 0 -2
y 2 0 -4 -2
Vậy cặp số (x,y) cần tìm là :
(2,2),(4,0),(0,-4),(-2,-2)
DD
Đoàn Đức Hà
Giáo viên
7 tháng 11 2021
\(\left(3a+2b\right)⋮17\Leftrightarrow9\left(3a+2b\right)⋮17\Leftrightarrow\left(27a-17a+18b-17b\right)⋮17\)
\(\Leftrightarrow\left(10a+b\right)⋮17\)
\(\left(3a+2b\right)⋮17\Leftrightarrow13\left(3a+2b\right)⋮17\Leftrightarrow\left(39a-2.17a+26b-17b\right)⋮17\)
\(\Leftrightarrow\left(5a+9b\right)⋮17\)
KA
7 tháng 11 2021
3a+2b).8+10a+b=24a+16a+10a+b=34a+17b chia hết cho 17
⇒(3a+2b).8+10a+b chia hết cho 17
Mà 3a+2b chia hết cho 17⇒(3a+2b).8 chia hết cho 17
⇒10a+b chia hết cho 17(đpcm)
b)Ta có :
xy+x-y=4
⇒x.(y+1)-(y+1)=3
⇒(x-1).(y+1)=3
Vì x,y ∈Z
⇒x-1,y+1∈Z
⇒x-1,y+1∈Ư(3)
Lập bảng giá trị
x -1 1 3 -1 -3
y+1 3 1 -3 -1
x 2 4 0 -2
y 2 0 -4 -2
Vậy cặp số (x,y) cần tìm là :
(2,2),(4,0),(0,-4),(-2,-2)
Giải thích các bước giải:
KA
2 tháng 11 2021
a)a) - Xét tổng :
(5a+8b)+2(−a+2b)(5a+8b)+2(-a+2b)
=5a+8b−2a+4b=5a+8b-2a+4b
=3a+12b⋮3=3a+12b⋮3
→(5a+8b)+2(−a+2b)⋮3→(5a+8b)+2(-a+2b)⋮3
mà 5a+8b⋮35a+8b⋮3
→2(−a+2b)⋮3→2(-a+2b)⋮3
mà (2,3)=1(2,3)=1
→−a+2b⋮3→-a+2b⋮3
b)b) - Xét tổng :
(5a+8b)+(10a+b)(5a+8b)+(10a+b)
=5a+8b+10a+b=5a+8b+10a+b
=15a+9b⋮3=15a+9b⋮3
→(5a+8b)+(10a+b)⋮3→(5a+8b)+(10a+b)⋮3
mà 5a+8b⋮35a+8b⋮3
→10a+b⋮3→10a+b⋮3
c)c) - Xét tổng :
(5a+8b)+(16b+a)(5a+8b)+(16b+a)
=5a+8b+16b+a=5a+8b+16b+a
=6a+24b⋮3=6a+24b⋮3
→(5a+8b)+(16b+a)⋮3→(5a+8b)+(16b+a)⋮3
mà 5a+8b⋮35a+8b⋮3
→16b+a⋮3→16b+a⋮3
6)6)
- Xét x<0x<0
2017x=2016x+x2017x=2016x+x
mà x<0x<0
⇒2016x+x<2016x⇒2016x+x<2016x
⇒2017x<2016x⇒2017x<2016x
- Xét x=0x=0
⇒2016x=2017x=0⇒2016x=2017x=0
hay 2016x=2017x2016x=2017x
- Xét x>0x>0
2017x=2016x+x2017x=2016x+x
mà x>0x>0
⇒2016x+x>2016x⇒2016x+x>2016x
⇒2017x>2016x⇒2017x>2016x
b)b)
- Xét x<0x<0
x2>0x2>0
5x<05x<0
⇒x2>0>5x⇒x2>0>5x
⇒x2>5x⇒x2>5x
- Xét x=0x=0
⇒x2=5x=0⇒x2=5x=0
hay x2=5xx2=5x
- Xét x>0x>0
x2=x.x<5x⇔x<5x2=x.x<5x⇔x<5
x2=x.x=5x⇔x=5x2=x.x=5x⇔x=5
x2=x.x>5x⇔x>5
DN
1
12 tháng 4 2015
a) ab + 5a - 7b = 68
=>ab + 5a - 7b - 35 = 68 - 35
a(b + 5) - 7b - 7 .5 = 33
a(b + 5) - 7(b + 5) = 33
(b + 5)(a - 7) = 33
Phần còn lại bạn lập bảng nhé!
b) 7a - ab + 2b = 20
=> 7a - 14 - ab + 2b = 20 - 14
7a - 2.7 - b(a - 2) = 6
7(a - 2) - b(a - 2) =6
(a - 2)(7 - b) = 6
Phần còn lại bạn cũng lập bảng nhé!
R
24 tháng 11 2021
\(a=0;1;2;3\) ở câu a
\(a=0;1;2;3;4;5;6;7\) ở câu b
\(a=0;1;2;3;4;5;6\) ở câu c
4 tháng 10 2015
taco;17achia het cho17
suy ra 17a+3a+2b chia het cho17
suy ra20a+2bchia het cho17
rút gọn cho 2
suyra 10a+b chia hết cho 17
vậy số dư là 0
TN
23 tháng 12 2021
a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
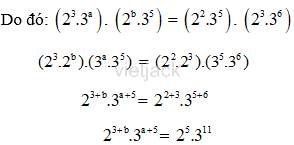
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
DN
11 tháng 11 2022
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6
1 tháng 1 2022
a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
11 tháng 1 2022
a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
ab + 2b = 17
=> b( a + 2 ) = 17
Ta có bảng sau:
Vậy x = 15; y = 1