Tìm 3 giá trị của y, sao cho:
3,5 < y < 3,51
Phải có lí do và lời giải thích
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 1 2019
Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
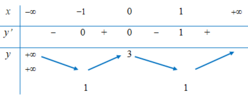
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
CM
3 tháng 4 2019
* Trước hết tìm giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).
- Tìm hoành độ của giao điểm:
2/5x + 1/2 = 3/5x - 5/2 ⇔ 1/5x = 6/2 ⇔ x = 15.
- Tìm tung độ giao điểm:
y = 2/5.15 + 1/2 = 6,5.
*Tìm k (bằng cách thay tọa độ của giao điểm vào phương trình ( d 3 ).
6,5 = k.15 + 3,5 ⇔ 15k = 3 ⇔ k = 0,2.
Trả lời: Khi k = 0,2 thì ba đường thẳng đồng quy tại điểm (15; 6,5).
MN
7 tháng 3 2020
\(ĐKXĐ:\hept{\begin{cases}y\ne2\\y\ne4\end{cases}}\)
\(\frac{y-1}{y-2}-\frac{3+y}{y-4}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Leftrightarrow\frac{\left(y-1\right)\left(y-4\right)-\left(3+y\right)\left(y-2\right)}{\left(y-2\right)\left(y-4\right)}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Leftrightarrow y^2-5y+4-y^2-y+6=-2\)
\(\Leftrightarrow-6y+10=-2\)
\(\Leftrightarrow-6y+12=0\)
\(\Leftrightarrow y=2\)(KTM)
Vậy tập nghiệm của phương trình là \(S=\varnothing\)
14 tháng 7 2016
a) |x-3,5| \(\ge\)0.
Vậy 0,5 - |x-3,5| \(\le\)0,5.
Vậy GTLN cùa A bằng 0,5 tại x-3,5 = 0 hay x = 3,5.
b) -|1,4-x| \(\le\)0.
Vậy -|1,4-x| - 2 \(\le\)-2.
Vậy GTLN của B bằng -2 tại 1,4 - x = 0 hay x = 1,4.
c) |3,4-x| \(\ge\)0.
Vậy 1,7 + |3,4-x| \(\ge\)1,7.
Vậy GTNN của C bằng 1,7 tại 3,4 - x = 0 hay x = 3,4.
d) |x+2,8| \(\ge\)0.
Vậy |x+2,8| - 3,5 \(\ge\)3,5.
Vậy GTNN của D bằng 3,5 tại x + 2,8 = 0 hay x = -2,8.
TN
14 tháng 7 2016
a)Ta thấy:- | x - 3,5|=<0
=> 0-5-| x - 3,5|=<0,5-0=0,5
=> A=<0,5
Dấu = khi x=3,5
Vậy...
Ta thấy:-|1,4-x|=<0
=>-|1,4-x|-2=<0-2=-2
=>B=<-2
Dấu = khi x=1,4
Vậy...
b)Ta thấy:|3,4-x|>=0
=>1,7+|3,4-x|>=1,7+0=1,7
=>C>=1,7
Dấu = khi x=3,4
Vậy....
Ta thấy:|x+2,8|>=0
=>|x+2,8|-3,5>=0-3,5=-3,5
=>D>=-3,5
Dấu = khi x=-2,8
Vậy....
14 tháng 7 2023
b: Để A nguyên thì 2n+3 chia hết cho n
=>3 chia hết cho n
=>n thuộc {1;-1;3;-3}
c: Th1: n=2
=>n+3=5(nhận)
TH2: n=2k+1
=>n+3=2k+4=2(k+2)
=>Loại
d: Gọi d=ƯCLN(2n+3;2n+5)
=>2n+5-2n-3 chia hết cho d
=>2 chia hết cho d
mà 2n+3 lẻ
nên d=1
=>PSTG
Các giá trị thỏa mãn đề của y có thể là 3,501; 3,505 và 3,509.
Dĩ nhiên vì 3,5 chính là 3,500 còn 3,51 chính là 3,510
Vì 3,500 < y < 3,510 nên chữ số hàng đơn vị và chữ số thập phân thứ nhất của y đều phải lần lượt 3 và 5.
Nhiệm vụ còn lại chỉ là tìm các số thỏa mãn 0 < số đó < 10 thôi.