giải phương trình: 2sin2x + \(\sqrt{ }\)3Sin2x = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
CM
28 tháng 11 2017
Đáp án B
Phương pháp:
Sử dụng phương pháp giải phương trình đẳng cấp bậc 2 đối với sin và cos bằng cách chia cả 2 vế phương trình cho cos 2 x .
CM
29 tháng 3 2019
Chia cả hai vế của bất phương trình cho 3 sin 2 x > 0 ta được: 2 3 sin 2 x + 3 . 1 9 sin 2 x ≥ m
Xét hàm số 2 3 sin 2 x + 3 . 1 9 sin 2 x
Hàm số f(x) là hàm nghịch biến.
Ta có
0 ≤ sin 2 x ≤ 1 ⇒ 2 3 1 + 3 . 1 9 1 ≤ f x ≤ 2 3 0 + 3 . 1 9 0
hay 1 ≤ f x ≤ 4
Vậy bất phương trình có nghiệm khi m ≤ 4
Đáp án A
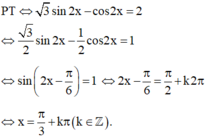
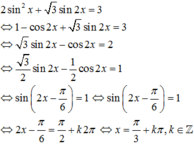
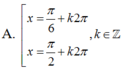
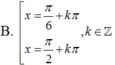
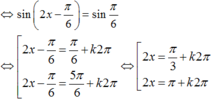
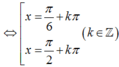
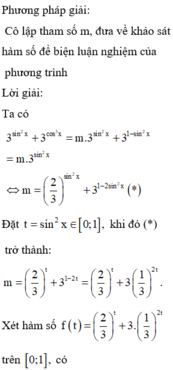
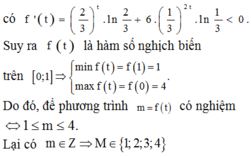
\(2\sin^2x+\sqrt{3}\sin2x=3\)
\(\Leftrightarrow2\sin^2x+2\sqrt{3}\sin x.\cos x=3\)
\(\Leftrightarrow2\tan^2x+2\sqrt{3}\tan x=\dfrac{3}{\cos^2x}\)
\(\Leftrightarrow2\tan^2x+2\sqrt{3}\tan x-3\left(1+\tan x\right)\)
\(\Leftrightarrow2\tan^2x+2\sqrt{3}\tan x-3-3\tan x=0\)
\(\Leftrightarrow2\tan^2x+\left(2\sqrt{3}-3\right)\tan x-3=0\)
Còn lại tự giải nhé