chứng minh (căn 10 + căn 17 +1) > căn 61
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{9-\sqrt{17}}\cdot\sqrt{9+\sqrt{17}}=\sqrt{\left(9-\sqrt{17}\right)\left(9+\sqrt{17}\right)}=\sqrt{9^2-\left(\sqrt{17}\right)^2}=\sqrt{81-17}\)
\(=\sqrt{64}=8.\)


\(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}\)
\(=\frac{1}{\sqrt{1}}+\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}\right)+\left(\frac{1}{\sqrt{5}}+...+\frac{1}{\sqrt{9}}\right)+...+\left(\frac{1}{\sqrt{82}}+...+\frac{1}{\sqrt{100}}\right)\)
\(>\frac{1}{\sqrt{1}}+\left(\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{4}}\right)+\left(\frac{1}{\sqrt{9}}+...+\frac{1}{\sqrt{9}}\right)+...+\left(\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\right)\)
\(>\frac{1}{1}+\frac{2}{2}+\frac{3}{3}+...+\frac{10}{10}=10\)


\(\sqrt{42-10\sqrt{17}}+\sqrt{33-8\sqrt{17}}\\ =\sqrt{\sqrt{25}^2-2.\sqrt{25}.\sqrt{17}+\sqrt{17}^2}+\sqrt{\sqrt{17}^2-2.\sqrt{17}.\sqrt{16}+\sqrt{16}^2}\\ =\sqrt{\left(5-\sqrt{17}\right)^2}+\sqrt{\left(\sqrt{17}-\sqrt{16}\right)^2}\\ =\left|5-\sqrt{17}\right|+\left|\sqrt{17}-\sqrt{16}\right|\\ =5-\sqrt{17}+\sqrt{17}-\sqrt{16}\\ =5-4\\ =1\)

\(\sqrt{99}<\sqrt{100}=10\)
\(\sqrt{50}+\sqrt{10}\)\(>\sqrt{49}+\sqrt{9}=7+3=10\)
Vậy \(\sqrt{50}+\sqrt{10}>\sqrt{99}\)

Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

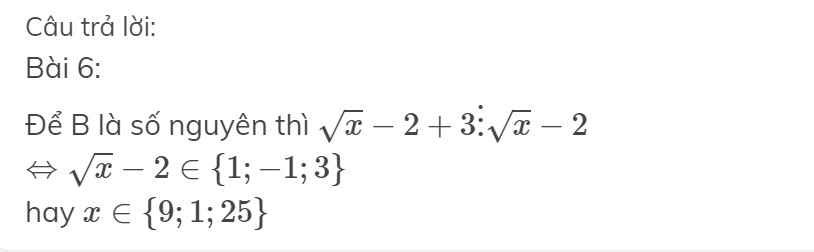
À cái này phải làm như thế này:
đpcm \(\Leftrightarrow\)\(\sqrt{10}+\sqrt{17}>\sqrt{61}-1\) \(\Leftrightarrow\left(\sqrt{10}+\sqrt{17}\right)^2>\left(\sqrt{61}-1\right)^2\)\(\Leftrightarrow27+2\sqrt{170}>62-2\sqrt{61}\) \(\Leftrightarrow2\left(\sqrt{170}+\sqrt{61}\right)>35\) \(\Leftrightarrow\sqrt{170}+\sqrt{61}>\dfrac{35}{2}\) \(\Leftrightarrow\left(\sqrt{170}+\sqrt{61}\right)^2>\dfrac{1225}{4}\) \(\Leftrightarrow231+2\sqrt{10370}>\dfrac{1225}{4}\) \(\Leftrightarrow2\sqrt{10370}>\dfrac{301}{4}\) \(\Leftrightarrow\sqrt{10370}>\dfrac{301}{8}\) \(\Leftrightarrow10370>\dfrac{90601}{64}\) \(\Leftrightarrow\dfrac{663680}{64}>\dfrac{90601}{64}\) (luôn đúng)
Vậy ta có đpcm
Tức là bạn sẽ chứng minh \(\sqrt{10}+\sqrt{17}>\sqrt{60}\) ???
Điều này \(\Leftrightarrow\left(\sqrt{10}+\sqrt{17}\right)^2>60\) \(\Leftrightarrow27+2\sqrt{170}>60\) \(\Leftrightarrow2\sqrt{170}>33\) \(\Leftrightarrow\sqrt{170}>\dfrac{33}{2}\Leftrightarrow170>\dfrac{1089}{4}\Leftrightarrow\dfrac{680}{4}>\dfrac{1089}{4}\) \(\Leftrightarrow680>1089\) ???
Bạn nên xem lại đề nhé.