mình cần gấp ạ! cảm ơn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

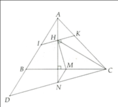

I'll only give you the solution. Draw the figure by yourself.
a) Because H is the orthocenter of the triangle ABC, we have \(AH\perp BC\). This means \(CM\perp NH\) or CM is a height of the triangle CHN.
On the other hand, \(HM\perp IK\) at H and \(CN//IK\). Therefore, \(HM\perp CN\) or HM is the second height of the triangle CHN.
So we have both HM and CM are the heights of the triangle CHN. Thus, NM must be the third height, which means \(NM\perp CH\), and that's what we must prove!
b) We simply get \(CH\perp AB\) because H is the orthocenter of the triangle ABC. Also, we have \(MN\perp CH\) (which is what we have already proved), therefore, \(MN//AB\) or \(MN//BD\).
Consider the triangle BCD, M is the midpoint of BC, \(MN//BD\) and \(N\in CD\). Thus, N must be the midpoint of CD, which means \(NC=ND\), and again, that's what we must prove!
c) Consider the triangle ADN, which has \(IH//DN\) . Thanks to the Thales theorem, we have \(\dfrac{HI}{ND}=\dfrac{AH}{AN}\)
Similarly, we have \(\dfrac{HK}{NC}=\dfrac{AH}{AN}\)
From these, we now have \(\dfrac{HI}{ND}=\dfrac{HK}{NC}\left(=\dfrac{AH}{AN}\right)\)
Guess what? We've already proved that \(ND=NC\), so, is there any problem when I write \(HI=HK\)?