Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
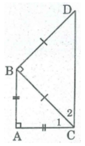
Vì ΔABC vuông cân tại A nên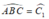 
Lại có: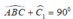 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên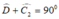 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.
a/ Xét tg ABC có
\(\widehat{ACB}=180^o-\widehat{BAC}-\widehat{ABC}\) (1)
\(\widehat{ABC}=\widehat{ACB}\) (2)
Xét tg BDM có
\(\widehat{BMD}=180^o-\widehat{BDM}-\widehat{ABC}\) (3)
Ta có \(\widehat{BAC}=\widehat{BDM}\) (4)
Từ (1) (2) (3) (4) \(\Rightarrow\widehat{ACB}=\widehat{BMD}\) => tg BDM cân tại D
=> DM=DB
Mà \(DB=DC=\dfrac{BC}{2}\)
\(\Rightarrow DM=DB=DC=\dfrac{BC}{2}\)
b/
Xét tg cân ABC có
\(\widehat{ACB}=\dfrac{180^o-\widehat{BAC}}{2}< \dfrac{180^o}{2}=90^o\)
=> \(\widehat{ACB}\) là góc nhọn \(\Rightarrow\widehat{DCN}\) là góc tù
=> DN>DC (trong tg cạnh đối diện với góc tù là cạnh có độ dài lớn nhất)
Mà DC=DM (cmt)
=> DN>DM