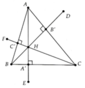
Cho tam giác ABC nhọn (AC>AB) đường cao AA',BB',CC' và trực tâm H. Gọi \(\left(O;\frac{BC}{2}\right)\). Từ A kẻ tiếp tuyến AM,AN tới (O). Gọi M' là giao điểm thứ hai của A'N với (O), K là giao điểm của OH và B'C'. CM:
a) M' là điểm dối xứng của M qua BC
b) Ba điểm M,H,N thẳng hàng
c) \(\frac{KB'}{KC'}=\left(\frac{HB'}{HC'}\right)^2\)