Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NA
Nguyễn acc 2
29 tháng 5 2022
Đúng(11)
Những câu hỏi liên quan
NV
1
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
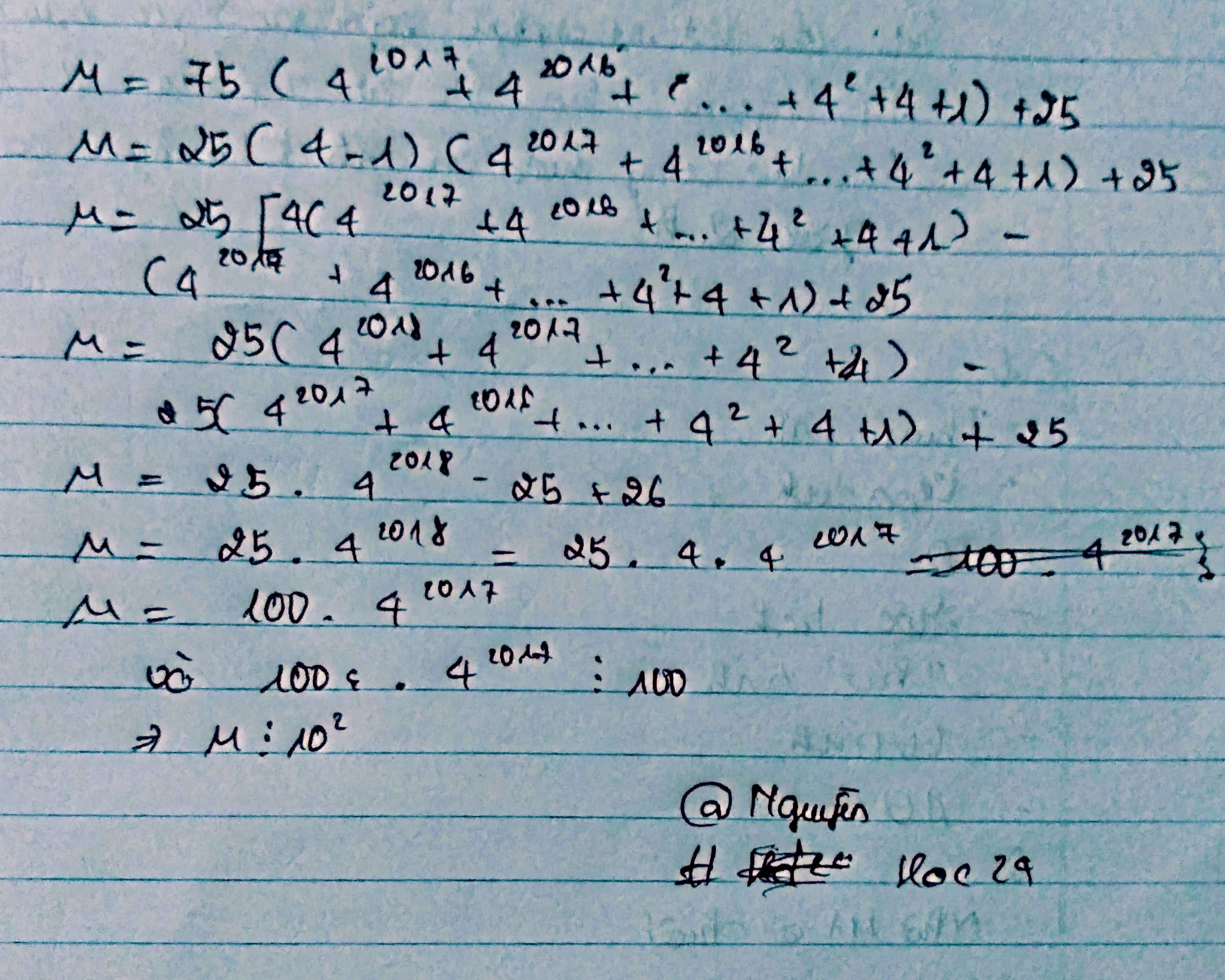
Lời giải:
Xét $A=4^{2021}+4^{2020}+...+4^2+4+1$
$4A=4^{2022}+4^{2021}+...+4^3+4^2+4$
$\Rightarrow 4A-A=4^{2022}-1$
$\Rightarrow 3A=4^{2022}-1$
$\Rightarrow M=75A+25=25(4^{2022}-1)+25=25.4^{2022}=100.4^{2021}\vdots 100$
Ta có đpcm.
17 tháng 4 2017
Chắc đặt nhầm lớp rồi
Ta có :\(B=4^{2004}+4^{2003}+...+4^2+4+1\)
\(4B=\left(4^{2004}+4^{2003}+...+4^2+4+1\right).4\)
\(4B=4^{2005}+4^{2004}+...+4^3+4^2+4\)
\(4B-B=\left(4^{2005}+4^{2004}+...+4^3+4^2+4\right)\)\(-\left(4^{2004}+4^{2003}+...+4+1\right)\)
\(3B=\left(4^{2005}-1\right)\)\(\Rightarrow\frac{4^{2005}-1}{3}\)
\(\Rightarrow A=75.\frac{4^{2005}-1}{3}+25\)
\(\Rightarrow A=25.\left(4^{2005}-1\right)+25\)
\(\Rightarrow A=25.\left(4^{2005}-1+1\right)\)
\(\Rightarrow A=25.4.4^{2004}\)
\(\Rightarrow A=100.4^{2004}\)
Mà 100 chia hết 100 nên \(100.4^{2004}\) chia hết cho 100
17 tháng 4 2017
B=4^0 + 4^1 +...+ 4^2004
4B=4^1+4^2+...+4^2005
3B=4^2004-4^0
B=(4^2004-4^0):3
Thay B vào ta có :
A=75.(4^2004-4^0):3+25
A=25.(4^2004-4^0)+25
A=25.4^2004
A=100.4^2003
Vậy A chia hết cho 100
R2
10 tháng 3 2020
THAM KHẢO LICK NÀY NHA :
https://h.vn/hoi-dap/question/783892.html
12 tháng 5 2022
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)
TD
3
DN
0