Vì sao diện tích tam giác đều cạnh là a lại là \(\dfrac{a^2\sqrt{3}}{4}\) vậy?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 5 2022
Đúng(3)
Những câu hỏi liên quan
16 tháng 1 2021
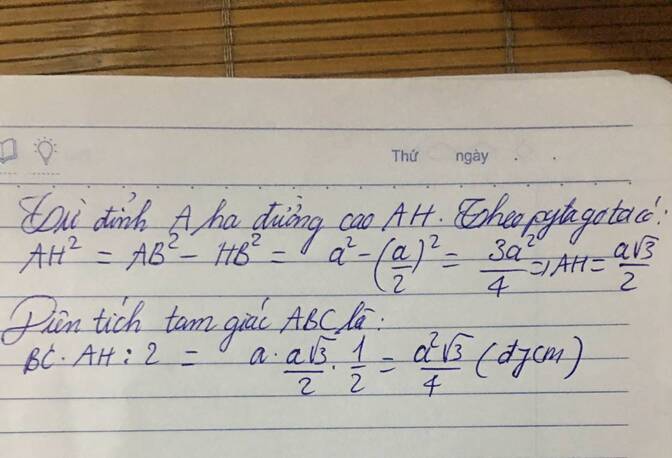
BĐT trên bị ngược dấu rồi.
Theo công thức Heron:
\(S=\dfrac{1}{4}\sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}\).
Do đó ta chỉ cần cm:
\(\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\leq a^2b^2+b^2c^2+c^2a^2\). (1)
Ta có \(\left(1\right)\Leftrightarrow a^4+b^4+c^4-a^2b^2-b^2c^2-c^2a^2\ge0\Leftrightarrow\dfrac{\left(a^2-b^2\right)^2}{2}+\dfrac{\left(b^2-c^2\right)^2}{2}+\dfrac{\left(c^2-a^2\right)^2}{2}\ge0\) (luôn đúng).
Do đó bđt ban đầu cũng đúng.
Đẳng thức xảy ra khi tam giác đó đều.
10 tháng 5 2022
sabc=2/3 sbcd vì có đáy ab =2/3 cd và có cc đều là chiều cao của hình thang
mà sabc +sbcd = sabcd. suy ra sabc = 2/3+2 =2/5 sabcd
mà smcd = 1/2 ht theo quy tắc ( bn tự tìm nhé đây là cô mình dạy)
sabc=2/5*1/2=1/5 smcd
smcd là : 48:1/5=240
b)khi điểm M di chuyển thì SMCD kg thay đổi vì các cạnh khác sẽ nối lại và bù lại cho phần chuyển ik
DD
Đoàn Đức Hà
Giáo viên
10 tháng 5 2022
a) \(S_{ABC}=\dfrac{2}{3}\times S_{MCD}\) (vì đường cao hạ từ \(C\) đến \(AB\) của tam giác \(ABC\) bằng đường cao hạ từ \(M\) đến \(CD\) của tam giác \(MCD\), \(AB=\dfrac{2}{3}\times CD\))
\(\Leftrightarrow S_{MCD}=\dfrac{3}{2}\times S_{ABC}=\dfrac{3}{2}\times48=72\left(cm^2\right)\)
b) Không thay đổi vì khoảng cách từ \(M\) đến \(CD\) không thay đổi.
T
17 tháng 1 2021
Bất đẳng thức ngược dấu rồi.
BĐT \(\Leftrightarrow\left(a+b+c\right)\prod\left(a+b-c\right)\le a^4+b^4+c^4\)
Đặt $\left\{ \begin{array}{l}a + b + c = 2s\\ab + bc + ca = {s^2} + 4Rr + {r^2}\\abc = 4sRr\end{array} \right.$
Bất đẳng thức cần chứng minh quy về:
\(16\,r{s}^{2} \left( R-2\,r \right) +2\,{s}^{2} \left( 5\,{r}^{ 2}+{s}^{2} -16\,Rr\right) +2\,{r}^{2} \left( 16\,{R}^{2}+8\,Rr+{r}^{2}-3\,{s} ^{2} \right) \geqslant 0\)
Đây là điều hiển nhiên.