Cho hình bình hành ABCD, góc B nhọn. Tứ C kẻ CM vuông góc với AB tại M, kẻ CN vuông góc với AD tại N. a) Chứng minh: ABMC O ADNC. b) Từ Bkẻ BH vuông góc với AD tại H. kẻ BK vuông góc với DC tại K. Chứng minh: DA.DH-DCDK DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔIDC vuông tại I và ΔKDB vuông tại K có
góc IDC chung
=>ΔIDC đồng dạng với ΔKDB
b: Xét ΔBHA vuông tại H và ΔBKC vuông tại K co
góc BAH=góc BCK
=>ΔBHA đồng dạng với ΔBKC
=>BH/BK=BA/BC
=>BK*BA=BH*BC

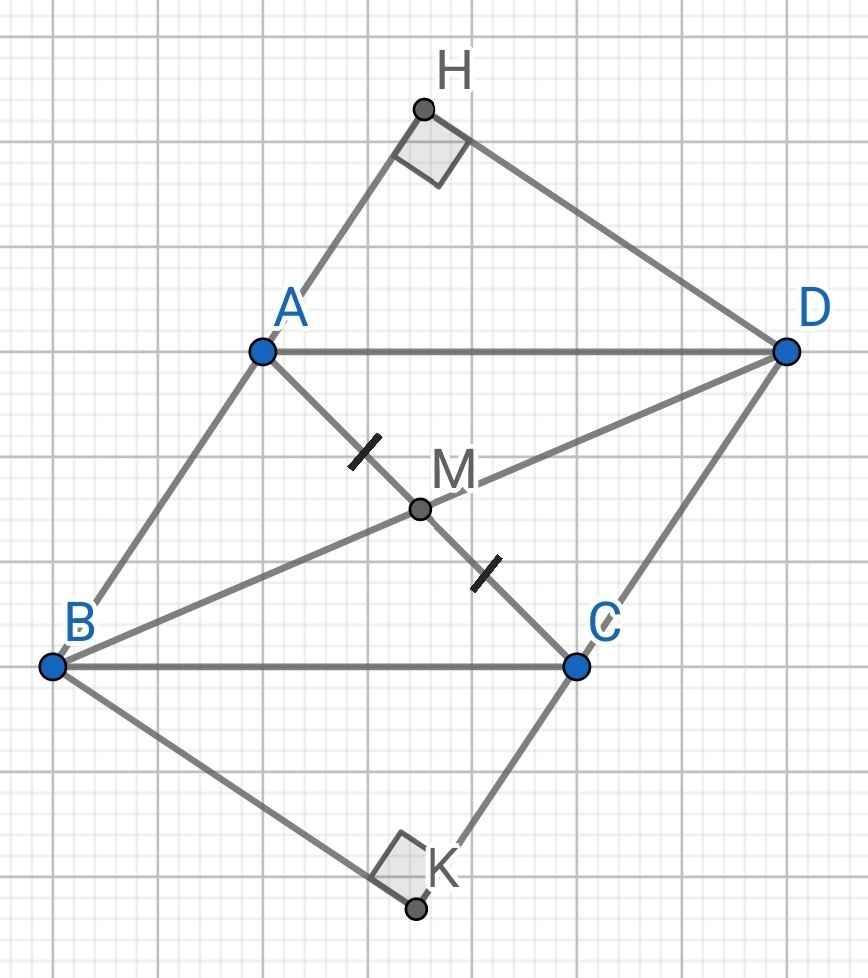 a) Do BM là đường trung tuyến của ∆ABC (gt)
a) Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
Do D và B đối xứng qua M (gt)
⇒ M là trung điểm của BD
Tứ giác ABCD có:
M là trung điểm của AC (cmt)
M là trung điểm của BD (cmt)
⇒ ABCD là hình bình hành
b) Do ABCD là hình bình hành (cmt)
⇒ AB // CD
Mà DH ⊥ AB
⇒ DH ⊥ AC
c) Do ABCD là hình bình hành
⇒ AB // CD
Mà BK ⊥ CD
⇒ BK ⊥ AB
⇒ ∠KBH = 90⁰
Tứ giác BHDK có:
∠BKD = ∠KBH = ∠BHD = 90⁰
⇒ BHDK là hình chữ nhật
Mà M là trung điểm BD
⇒ M là trung điểm của HK
⇒ M, H, K thẳng hàng
Do đó chứng minh MH ⊥ MK là sai. Em xem lại đề ở câu c nhé

a) Ta có AO là trung tuyến nên OC = OB.
Lại có OD = OA nên ABDC là hình bình hành ( Hai đường chéo cắt nhau tại trung điểm mỗi đường)
b) Ta thấy \(\Delta CKO=\Delta BHO\) ( Cạnh huyền - góc nhọn) nên CK = BH ( Hai cạnh tương ứng)
Mà CK và BH lại cùng vuông góc với AD nên chúng song song.
Vậy thì tứ giác BHCK là hình bình hành ( Cặp cạnh đối song song và bằng nhau)
c) Do CN // BM; AC // BD nên \(\widehat{ACN}=\widehat{DBM}\Rightarrow\Delta ACN=\Delta DBM\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CN=BM\)
Tứ giác CMBN có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Vậy BC giao MN tại trung điểm mỗi đường. O là trung điểm BC nên O cũng là trung điểm MN. Vậy M, N, O thẳng hàng.
a: Xét ΔBMC vuông tại M và ΔDNC vuông tại N có
góc B=góc D
=>ΔBMC đồng dạng vớiΔDNC
b: Bạn ghi lại đề đi bạn