cho x thuộc Z. CM x200+x100+1 chia hết cho x4+x2+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49


\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
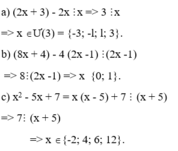
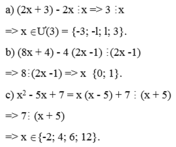
Ta có
x200 = (x200 + x198 + x196) + (- x198 - x196 - x194) + ...+ x2 = (x4 + x2 + 1)A(x) + x2
Tương tự
x100 = (x4 + x2 + 1)B(x) + x4
Từ đó ta có
x200 + x100 + 1 = (x4 + x2 + 1)A(x) + x2 + (x4 + x2 + 1)B(x) + x4 + 1
= (x4 + x2 + 1)C(x) chia hết cho x4 + x2 + 1
biến đổi x^200+x^100+1 ra sao nhỉ