giải giúp mình phương trình này ạ
K
Khách
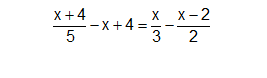
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
2
2
14 tháng 5 2022
`x^2+\sqrt{x^2+20}=22`
`<=>x^2+20+\sqrt{x^2+20}-42=0`
Đặt `\sqrt{x^2+20}=t` `(t > 0)` khi đó ta có ptr:
`t^2+t-42=0`
`<=>t^2+7t-6t-42=0`
`<=>t(t+7)-6(t+7)=0`
`<=>(t+7)(t-6)=0`
`<=>` $\left[\begin{matrix} t=-7\text{ (ko t/m)}\\ t=6\text{ (t/m)}\end{matrix}\right.$
`@ t=6=>\sqrt{x^2+20}=6`
`<=>x^2+20=36`
`<=>x^2=16`
`<=>x=+-4`
Vậy `S={+-4}`
11 tháng 10 2023
Để giải phương trình \(x^2 + \sqrt{x^2 + 20} = 22\), bạn có thể làm theo các bước sau:
1. Trừ 22 từ cả hai bên của phương trình để đưa các thuật ngữ chứa x về cùng một bên:
\(x^2 + \sqrt{x^2 + 20} - 22 = 0\)
2. Bây giờ, chúng ta có một phương trình bậc hai dạng căn bậc hai. Để giải phương trình này, ta sẽ giải quyết từng phần:
\(x^2 + \sqrt{x^2 + 20} = 22\)
3. Bây giờ, ta sẽ loại bỏ căn bậc hai bằng cách đưa nó về phía bên kia của phương trình:
\(x^2 = 22 - \sqrt{x^2 + 20}\)
4. Bình phương cả hai phía của phương trình:
\(x^4 = (22 - \sqrt{x^2 + 20})^2\)
5. Giải phương trình bậc bốn này:
\(x^4 = (22 - \sqrt{x^2 + 20})^2\)
\(x^4 = 484 - 44\sqrt{x^2 + 20} + (x^2 + 20)\)
6. Đưa các thuật ngữ chứa \(x^2\) về cùng một bên:
\(x^4 - x^2 - 464 = - 44\sqrt{x^2 + 20}\)
7. Bình phương cả hai phía của phương trình:
\((x^4 - x^2 - 464)^2 = (- 44\sqrt{x^2 + 20})^2\)
\(x^8 - 2x^6 - 23x^4 + 912x^2 + 464^2 = 1936x^2 + 20\)
8. Rút gọn và sắp xếp phương trình:
\(x^8 - 2x^6 - 23x^4 + 1916x^2 + 464^2 - 20 = 0\)
9. Đây là một phương trình bậc tám, và giải nó có thể phức tạp. Bạn có thể sử dụng phần mềm máy tính hoặc các công cụ trực tuyến để tìm các nghiệm của phương trình này. Giải nghiệm này là một phương trình bậc cao và cần một giải thuật đặc biệt.
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
\(\Leftrightarrow2sin^3x+1-sin^2x-1=0\)
\(\Leftrightarrow sin^2x\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
8 tháng 11 2021
1) ĐKXĐ: \(x\ge-5\)
\(pt\Leftrightarrow x+5=9\Leftrightarrow x=9-5=4\left(tm\right)\)
2) ĐKXĐ: \(x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\sqrt{x-3}=6\)
\(\Leftrightarrow2\sqrt{x-3}=6\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\Leftrightarrow x=12\left(tm\right)\)
3) ĐKXĐ: \(x\ge-1\)
\(pt\Leftrightarrow\sqrt{\left(x+1\right)^2}-2\sqrt{x+1}=0\)
\(\Leftrightarrow x+1-2\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
HH
1
XO
17 tháng 4 2022
x3 - 6xy + y3 = 8
<=> (x + y)3 - 3xy(x + y) - 6xy + 8 = 16
<=> (x + y + 2)(x2 + y2 - xy - 2x - 2y + 4) = 16
<=> \(\left(x+y+2\right)\left[\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\right]=16\)
Nhận thấy \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\ge0\)
=> x + y + 2 > 0
Khi đó 16 = 1.16 = 2.8 = 4.4
Lập bảng
| x + y + 2 | 1 | 16 | 4 | 2 | 8 | |
| \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\) | 16 | 1 | 4 | 8 | 2 | |
| x | ||||||
| y | | |
Đến đó bạn thế x qua y rồi làm tiếp nha
19 tháng 8 2021
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
TN
19 tháng 9 2016
\(3x^4+4x^3-3x^2-2x+1=0\)
\(\Leftrightarrow3x^4+x^3-x^2+3x^3+x^2-x-3x^2-x+1=0\)
\(\Leftrightarrow x^2\left(3x^2+x-1\right)+x\left(3x^2+x-1\right)-\left(3x^2+x-1\right)=0\)
\(\Leftrightarrow\left(x^2+x-1\right)\left(3x^2+x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+x-1=0\left(1\right)\\3x^2+x-1=0\left(2\right)\end{cases}}\)
- \(\Delta_{\left(1\right)}=1^2-\left(-4\left(1.1\right)\right)=5\)
\(\Leftrightarrow x_{1,2}=\frac{-1\pm\sqrt{5}}{2}\left(tm\right)\)
- \(\Delta_{\left(2\right)}=1^2-\left(-4\left(3.1\right)\right)=13\)
\(x_{1,2}=\frac{-1\pm\sqrt{13}}{6}\left(tm\right)\)
18 tháng 9 2021
\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x^2-2x}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x^2-2x\)
\(\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\)
18 tháng 9 2021
Cho mình sửa lại nhé:
\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x-2\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
0H
giải phương trình này giúp em với ạ
1
3 tháng 3 2022
\(\dfrac{x^2+2}{x^2+4}=0\\ \Leftrightarrow x^2+2=0\)
Ta có: \(x^2\ge0;2>0\Rightarrow x^2+2>0\)
Vậy pt vô nghiệm
\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)\(\Leftrightarrow\)\(\dfrac{x+4}{5}-\dfrac{5x}{5}+\dfrac{20}{5}=\dfrac{2x}{6}-\dfrac{3\left(x-2\right)}{6}\)
\(\Leftrightarrow\)\(\dfrac{-4x+24}{5}=\dfrac{-x+6}{6}\Leftrightarrow6\cdot\left(-4x+24\right)=5\cdot\left(-x+6\right)\)
\(\Leftrightarrow\)-24x+144=-5x+30\(\Leftrightarrow\)-24x+5x=30-144\(\Leftrightarrow\)-19x=-114\(\Leftrightarrow\)x=6