Biết rằng a / b = -2.4 / 3.8 và 2a + b = -6 . Giá trị của a + b = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: a : b = -2,4 : 3,8
hay \(\frac{a}{b}=\frac{-2,4}{3,8}\) => \(\frac{a}{-2,4}=\frac{b}{3,8}\) => \(\frac{2a}{-4,8}=\frac{b}{3,8}\)
và 2a + b = -6
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{-2,4}=\frac{b}{3,8}\) = \(\frac{2a}{-4,8}=\frac{b}{3,8}\) = \(\frac{2a+b}{-4,8+3,8}\) = \(\frac{-6}{-1}=6\)
- \(\frac{a}{-2,4}=6\) => a = 6.(-2,4) = -14,4
- \(\frac{b}{3,8}=6\) => b = 6 . 3,8 = 22,8
Vậy a = -14,4
b = 22,8
Chúc bạn học tốt!

Biết rằng a:b = 3:5 và 3a-b=17,2 . Giá trị của a+b= 34.4
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Biết rằng a:b = -2,4:3,8 và 2a+b=-6 . Giá trị của a+b=8.4
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Biết rằng a:b = 3:5 và 3a-b=17,2 . Giá trị của a+b= 34.4
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Biết rằng a:b = -2,4:3,8 và 2a+b=-6 . Giá trị của a+b=8.4
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
chúc bn hok tốt @_@

a : b = -2,4 : 3,8 = -1,2/1,9 = -12/19
=> a = -12b/19
2a+b=6
2 * -12b/19 + b = 6
-24b/19 +b = 6
-5b/19 = 6
-5b = 114
b = -22,8

Giải:
Ta có: \(\frac{a}{b}=\frac{-2,4}{3,8}\Rightarrow\frac{a}{-2,4}=\frac{b}{3,8}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{-2,4}=\frac{b}{3,8}=\frac{2a}{-4,8}=\frac{2a+b}{-4,8+3,8}=\frac{-6}{-1}=6\)
+) \(\frac{a}{-2,4}=6\Rightarrow a=-14,4\)
+) \(\frac{b}{3,8}=6\Rightarrow b=22,8\)
\(\Rightarrow a+b=-14,4+22,8=8,4\)
Vậy a + b = 8,4
Ta có : \(\frac{a}{b}=\frac{-2,4}{3,8}\Rightarrow\frac{a}{3,8}=\frac{b}{-2,4}\) và \(2a+b=-6\)
Áp dung tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{a}{3,8}=\frac{b}{-2,4}=\frac{2a+b}{2.3,8+-2,4}=\frac{-6}{5,2}=-\frac{15}{13}\)
\(\Rightarrow\begin{cases}\frac{a}{3,8}=-\frac{15}{13}\Rightarrow a=-\frac{15}{13}.3,8=-\frac{57}{13}\\\frac{b}{-2,4}=-\frac{15}{13}\Rightarrow b=-\frac{15}{13}.-2,4=\frac{36}{13}\end{cases}\)
Vậy .............


Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà a > b > 0 => M = 3
Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà \(a>b>0\Rightarrow M=3\)

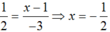 .
.
Bài này có trên violympic 7 vòng 5 đúng không
Bạn spam phải không?