2/7 x y - 1/4 x y = 3/7
giúp tui với! Help meeeeeeeeeeeeeeeeee!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 6 2017
( 2 x y + 2/15 ) x 3 = 4/5
( 2 x y + 2/15 ) = 4/5 : 3
( 2 x y + 2/15 ) = 4/15
2 x y = 4/15 - 2/15
2 x y = 2/15
y = 2/15 :2
y = 1/15
DP
7 tháng 6 2017
(2 x y + 2/15) x 3 = 4/5
2 x y + 2/15) = 4/5 : 3
2 x y + 2/15 = 4/15
2 x y = 4/15 - 2/15
2 x y = 2/15
y = 2/15 : 2
y = 1/15
7/9 x (2 - 1/3 x y) = 14/15
(2 - 1/3 x y) = 14/15 : 7/9
(2 - 1/3 x y) = 6/5
2 - y = 6/5 x 1/3
2 - y = 2/5
y = 2/5 + 2
y = 12/5
4/21 + 5 x y - 8/7 = 1/3
4/21 + 5 x y = 1/3 + 8/7
4/21 + 5 x y = 31/21
5 x y = 31/21 - 4/21
5 x y = 9/7
y = 9/7 : 5
y = 9/35
7/12 x y - 3/12 x y = 5
y x (7/12 - 3/12) = 5
y x 1/3 = 5
y = 5 : 1/3
y = 15
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 9 2021
ta có :
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{10}{2z+8}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{10}{2z+8}=\frac{7+3+10}{2x+2+2y-4+2z+8}=\frac{20}{2\left(x+y+z\right)+6}=\frac{20}{40}=\frac{1}{2}\)
\(\Rightarrow\hept{\begin{cases}2x+2=14\\2y-4=6\\2z+8=10\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=5\\z=1\end{cases}}\)
2 tháng 9 2021
ta có
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{5}{z+4}=\frac{7+3}{2x+2y+2-4}=\frac{10}{2x+2y+2-4}=\frac{10}{2\left(x+y\right)-4}=\frac{5}{x+y-1}\)
\(=\frac{10}{17-1+4}=\frac{10}{20}=\frac{1}{2}\)
từ đó bạn tính ra nha
3 tháng 12 2023
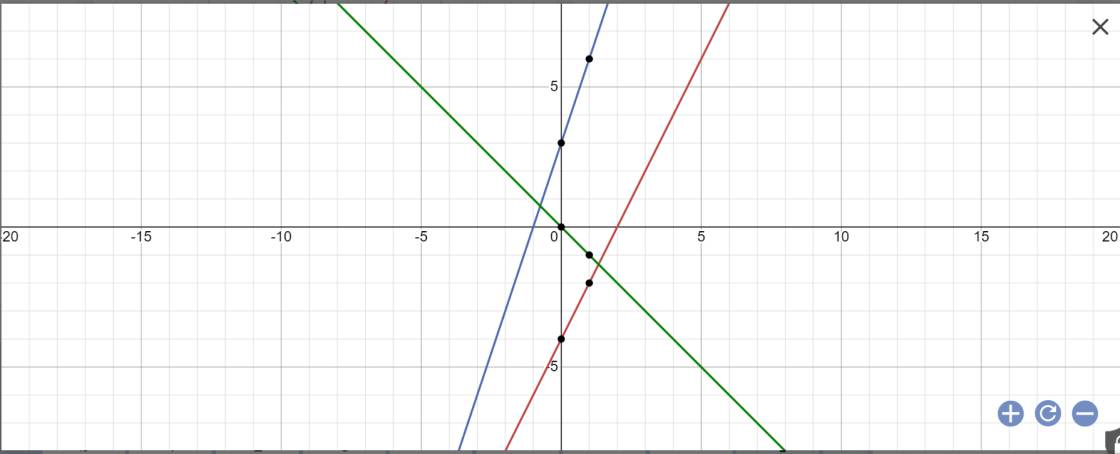
*Bảng giá trị:
| x | -1 | 0 | 1 |
| y=2x-4 | -6 | -4 | -2 |
| y=3x+3 | 0 | 3 | 6 |
| y=-x | 1 | 0 | -1 |
*Vẽ đồ thị:
NN
2
TP
25 tháng 12 2022
\((2x-1)^2+(x+3)^2-5(x+7)(x-7)=0\)
\(< =>4x^2-4x+1+x^2+6x+9-5\left(x^2-7^2\right)=0\\ < =>4x^2-4x+1+x^2+6x+9-5x^2+245=0\\ < =>2x+255=0\\ < =>2x=-255=>x=\dfrac{-255}{2}\)
Vậy \(x=\dfrac{-255}{2}\)
DX
25 tháng 12 2022
\(\Rightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)
\(\Rightarrow2x+255=0\Rightarrow2x=-255\Rightarrow x=-\dfrac{255}{2}\)
4 tháng 1
a: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7x=14\\2x+y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=5-2x=5-2\cdot2=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}-x+2y=2\\2x-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+4y=4\\2x-y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=3\\x-2y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\x=-2+2y=-2+2\cdot1=0\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}2x-y=13\\y-5=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=13\\y=-7+5=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=y+13=-2+13=11\\y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{11}{2}\\y=-2\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}3x+y=8\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y=24\\2x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=25\\3x+y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{25}{11}\\y=8-3x=8-3\cdot\dfrac{25}{11}=8-\dfrac{75}{11}=\dfrac{13}{11}\end{matrix}\right.\)
\(y\times\left(\dfrac{2}{7}-\dfrac{1}{4}\right)=\dfrac{3}{7}\)
\(y=\dfrac{3}{7}:\dfrac{1}{28}=12\)
\(y\times\left(\dfrac{2}{7}-\dfrac{1}{4}\right)=\dfrac{3}{7}\)
\(y\times\dfrac{1}{28}=\dfrac{3}{7}\)
\(y=\dfrac{3}{7}:\dfrac{1}{28}=\dfrac{3\times28}{7}=12\)